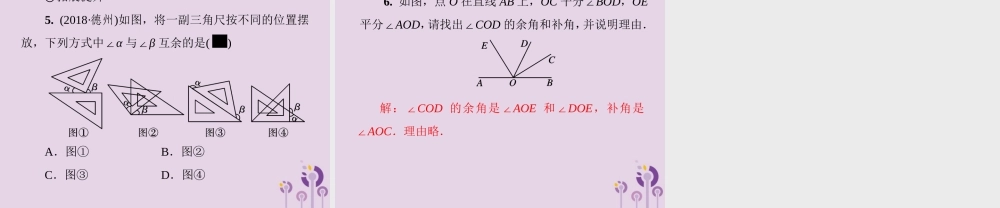
第二章相交线与平行线2.1 两条直线的位置关系第 1 课时两条直线相交所成的角◎知识梳理 1. 两条直线相交有且只有 交点;在同一平面内, 的两条直线叫做平行线. 2. 如果两个角的和是 ,那么称这两个角互为余角.如果两个角的和是 180°,那么称这两个角 . 两条相交直线中,有公共顶点且两边互为反向延长线的两个角叫做 . 一个 不相交 直角 互为补角 对顶角 3. 同角或 的余角相等; 或等角的补角相等;对顶角 . 等角 同角 相等 ◎自主检测 知识点:对顶角的识别与性质 1. 下列图形中,1∠ 与2∠ 是对顶角的是( ) D 2. (2018·邵阳)如图所示,直线 AB,CD 相交于点 O,已知∠AOD=160°,则∠BOC 的大小为( ) A.20° B.60° C.70° D.160° D 知识点:余角与补角的性质 3. 若∠A=65°,则么∠A 的余角等于 °;若1∠与2∠互补,则1∠ +2∠ = °;若∠B=α,则∠B的余角= ,∠B 的补角= . 4. 若∠A+∠B=90°,∠B+∠C=90°,则∠A ∠C,理由是 . 25 180 90° - α 180° - α = 同角的余角相等 探究:如图所示,直线 AB,CD 相交于点 O,作∠DOE=∠BOD, ∠DOE+∠FOE=90°. (1)写出∠DOE 的补角; (2)写出∠AOC 的对顶角和余角; (3)若∠AOF 是∠AOC 的 2 倍,求∠BOD 的度数. 解:(1)∠DOE 的补角是∠COE 和∠AOD; (2)∠AOC 的对顶角是∠BOD,余角是∠AOF 和∠EOF; (3)设∠AOC=x,由 x+2x=90°,得∠AOC=30°=∠BOD. 探究: 如图所示,三条直线 AB,CD,EF 相交于点 O,∠AOF∠FOB=31∶ ,∠AOC=90°,求∠EOC的度数. 解:设∠FOB=x°, 得 3x+x=180, 求得∠FOB=45°, 所以∠AOE=45°, ∠EOC=45°. ◎基础训练 1. 如图,∠AOB=∠COD=90°,则下列叙述中正确的是( ) A.∠AOC=∠AOD B.∠AOD=∠BOD C.∠AOC=∠BOD D.∠AOC+∠BOD=90° C 2. (2018·贺州)如图,下列各组角中,互为对顶角的是( ) A.1∠ 和2∠ B.1∠ 和3∠ C.2∠ 和4∠ D.2∠ 和5∠ A 3. 若1∠ +3∠ =180°,2∠ +4∠ =180°,且1∠ =2∠ ,则4∠ 3∠ ,理由是 . = 等角的补角相等 4. 如图,直线 AB,CD 交于点 O,射线 OM 平分∠AOC,若∠BOD=76°,求∠COM 和∠BOM 的度数. 解:∠COM =38°, ∠BOM =142°. ◎拓展提升 5. (2018·德州)如图,将一副三角尺按不同的位置摆放,下列方式中∠α 与∠β 互余的是( ) A.图① B.图② C.图③ D.图④ A 6. 如图,点 O 在直线 AB 上,OC 平分∠BOD,OE平分∠AOD,请找出∠COD 的余角和补角,并说明理由. 解:∠COD 的余角是∠AOE 和∠DOE,补角是∠AOC.理由略.