指数函数 课件VIP免费

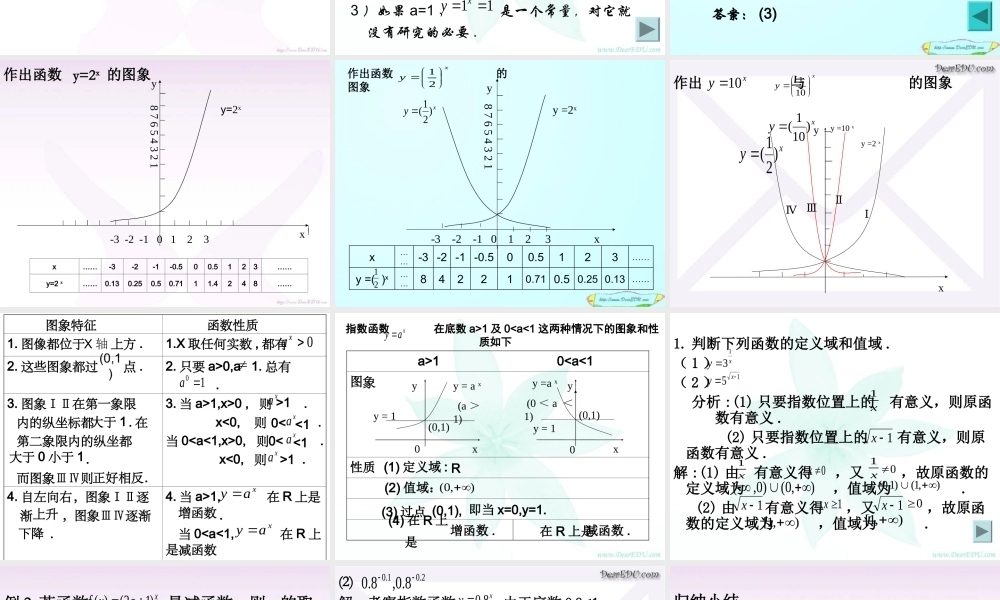
指数函数指数函数指数函数指数函数指数函数 nanmana0a nma复习：n 个*)(Nnaaaa)0(1a*),0(1Nnaa n)1*,,,0(nNnmaanm)1*,,,0(1nNnmaanm问题 一把尺子第一次截去它的一半，第二次截去剩余部分的一半，第三次截去第二次剩余部分的一半，依次截下去，问截的次数与剩下的尺子之间的关系 . 次数 长度 1 次 2 次 3 次 ...... ...... x 次 212121 221 212121321 212121x21x 个 一把尺子截 x 次后，得到的尺子的长度 y 与 x 的关 系式是 自变量 x 作为指数，底数为 ，是一个大于 0 且小于 1 的常数 . 像这样的函数我们把它叫做指数函数 . xy 2121 我们要求 a>0,a 1 ，是因为： 1) 如果 a=0, 当 x>0 时， 恒等于 0 ， 当 x 0 时， 无意义 . 2 ）如果 a<0 ，比如 ，这时对于 等，在实数范围内函数值不存在 . 3 ）如果 a=1 ， 是一个常量，对它就 没有研究的必要 .xaxaxy4,41x,21x11 xy指数函数定义 一般地，函数 (a>0,a 1) 叫做指数函数，其中 x 是自变量 . 函数的定义域是 R.xay  例 : 下列函数是不是指数函数 ? xy32)2(13)1(xy)0()32()3(2aaayx13)4(xy33x答案： (3)x……-3-2-1-0.500.5123……y=2 x……0.130.250.50.7111.4248……xy-3 -2 -1 0 1 2 3 8 7 6 5 4 3 2 1作出函数 y=2x 的图象y=2x…………0.1330.2520.510.710.5102-0.52-14-28-3…………y =( )xx21 -3 -2 -1 0 1 2 3yy =2xx8 7 6 5 4 3 2 1 xy)21(xy 21作出函数 的图象作出 与 的图象xyy =10 xⅠⅡⅢⅣxy)21(xy)101(y =2 xxy10xy 101 图象特征 函数性质1. 图像都位于 上方 .1.X 取任何实数 , 都有 2. 这些图象都过 点 . 2. 只要 a>0,a 1. 总有 . 3. 图象ⅠⅡ在第一象限 内的纵坐标都 . 在 第二象限内的纵坐都 . 而图象ⅢⅣ则 .3. 当 a>1,x>0 , 则 . x<0, 则 .当 00, 则 . x<0, 则 .4. 自左向右，图象ⅠⅡ逐 渐 ，图象ⅢⅣ逐渐 .4. 当 a>1, 在 R 上是 . 当 01 >1 <1 <1 ...