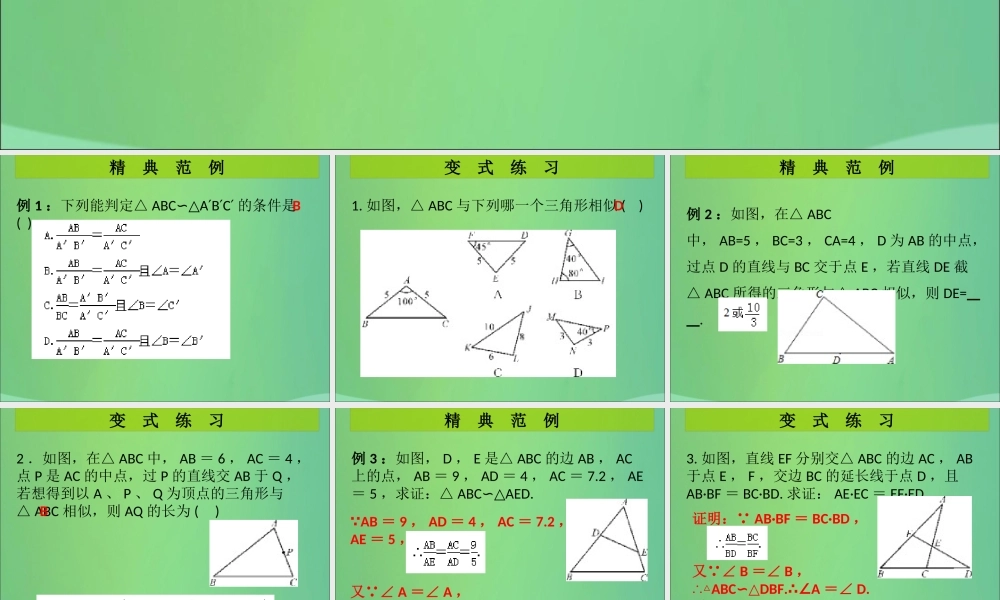
第 6 课时探索三角形相似的条件( 2 )巩固提高精典范例(变式练习)第四章 图形的相似例 1 :下列能判定△ ABCA B C∽△ ′ ′ ′ 的条件是( )精 典 范 例B1. 如图,△ ABC 与下列哪一个三角形相似 ( )变 式 练 习D例 2 :如图,在△ ABC中, AB=5 , BC=3 , CA=4 , D 为 AB 的中点,过点 D 的直线与 BC 交于点 E ,若直线 DE 截△ ABC 所得的三角形与△ ABC 相似,则 DE= .精 典 范 例2 .如图,在△ ABC 中, AB = 6 , AC = 4 ,点 P 是 AC 的中点,过 P 的直线交 AB 于 Q ,若想得到以 A 、 P 、 Q 为顶点的三角形与△ ABC 相似,则 AQ 的长为 ( )变 式 练 习B例 3 :如图, D , E 是△ ABC 的边 AB , AC上的点, AB = 9 , AD = 4 , AC = 7.2 , AE= 5 ,求证:△ ABCAED.∽△精 典 范 例 AB = 9 , AD = 4 , AC = 7.2 ,AE = 5 ,又 ∠ A =∠ A ,∴△ABCAED.∽△3. 如图,直线 EF 分别交△ ABC 的边 AC , AB于点 E , F ,交边 BC 的延长线于点 D ,且AB·BF = BC·BD. 求证: AE·EC = EF·ED.变 式 练 习证明: AB·BF = BC·BD ,又 ∠ B =∠ B ,∴△ABCDBF.A∽△∴∠=∠ D.又 ∠ AEF =∠ DEC ,∴△ AEFDEC.∽△ 即 AE·EC = EF·ED.巩 固 提 高4. 如图, D 是△ ABC 一边 BC 上一点,连接AD ,使△ ABCDBA∽△的条件是 ( ) A . ACBC∶= AD∶B DB . ACBC∶= ABAD∶ C . AB2 = CD·BC D . AB2 = BD·BCD 巩 固 提 高5 .如图 1 ,图 2 中各有两个三角形,其边长和角的度数已在图上标注,图 2 中 AB 、 CD 交于 O 点,对于各图中的两个三角形而言,下列说法正确的是 ( ) A .只有图 1 相似 B .只有图 2 相似 C .都相似 D .都不相似C巩 固 提 高6. 如图,△ ABC 中,∠ A = 78° , AB =4 , AC = 6. 将△ ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )C巩 固 提 高7. 下列 4×4 的正方形网格中,小正方形的边长均为 1 ,三角形的顶点都在格点上,则与△ ABC 相似的三角形所在的网格图形是图 .巩 固 提 高8 .在△ ABC 和△ A B C′ ′ ′ 中,若∠ B ...