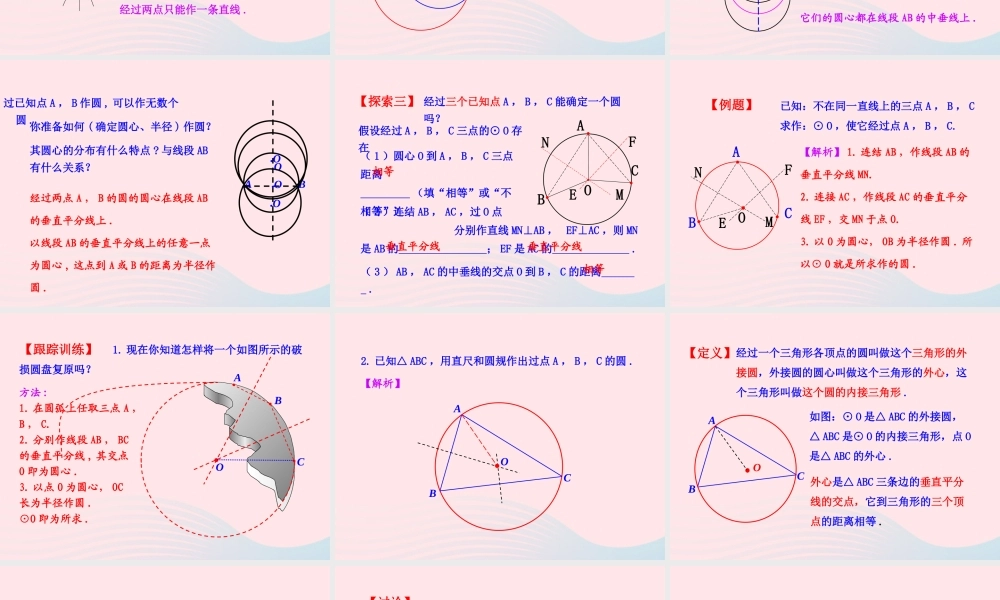
3.1.3 过不在同一直线上的三点作圆1. 了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法 .2 .了解三角形的外接圆 , 三角形的外心等概念 .3 .经历不在同一直线上的三个点确定一个圆的探索过程,培养学生的探索能力 .一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?要确定一个圆必须满足几个条件 ?想一想1. 过一点可以作几条直线?2. 过几点可确定一条直线?过几点可以确定一个圆呢?经过两点只能作一条直线 .●A●A●B经过一点可以作无数条直线;经过一个已知点 A 能确定一个圆吗 ?A经过一个已知点能作无数个圆【探索一】经过两个已知点 A , B 能确定一个圆吗 ?AB 经过两个已知点 A , B 所作的圆的圆心在怎样的一条直线上 ?它们的圆心都在线段 AB 的中垂线上 . 经过两个已知点 A , B 能作无数个圆 .【探索二】过已知点 A , B 作圆 , 可以作无数个圆 .经过两点 A , B 的圆的圆心在线段 AB的垂直平分线上 .以线段 AB 的垂直平分线上的任意一点为圆心 , 这点到 A 或 B 的距离为半径作圆 .你准备如何 ( 确定圆心、半径 ) 作圆?其圆心的分布有什么特点 ? 与线段 AB有什么关系?●A●B●O●O●O●O经过三个已知点 A , B , C 能确定一个圆吗?假设经过 A , B , C 三点的⊙ O 存在( 1 )圆心 O 到 A , B , C 三点距离 (填“相等”或“不相等”) .( 2 )连结 AB , AC ,过 O 点 分别作直线 MN⊥AB , EF⊥AC ,则 MN是 AB 的 ; EF 是 AC 的 .( 3 ) AB , AC 的中垂线的交点 O 到 B , C 的距离 .NMFE OABC相等垂直平分线垂直平分线相等【探索三】已知:不在同一直线上的三点 A , B , C求作:⊙ O ,使它经过点 A , B , C.【解析】 1. 连结 AB ,作线段 AB 的垂直平分线 MN.2. 连接 AC ,作线段 AC 的垂直平分线 EF ,交 MN 于点 O.3. 以 O 为圆心, OB 为半径作圆 . 所以⊙ O 就是所求作的圆 .ONMFEABC【例题】 1. 现在你知道怎样将一个如图所示的破损圆盘复原吗?方法 :1. 在圆弧上任取三点 A ,B , C.2. 分别作线段 AB , BC的垂直平分线 , 其交点O 即为圆心 .3. 以点 O 为圆心, OC长为半径作圆 .⊙O 即为所...