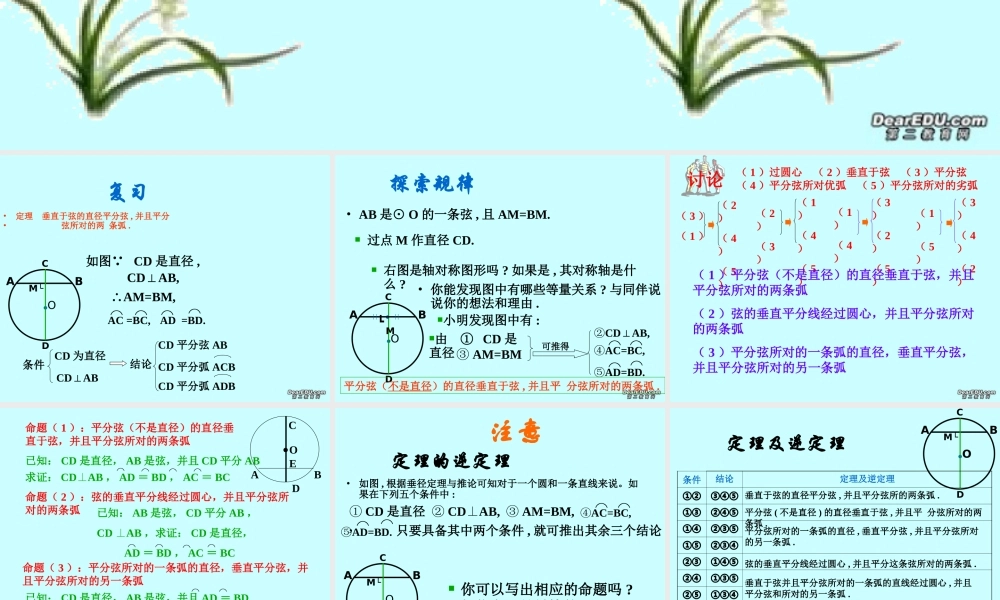
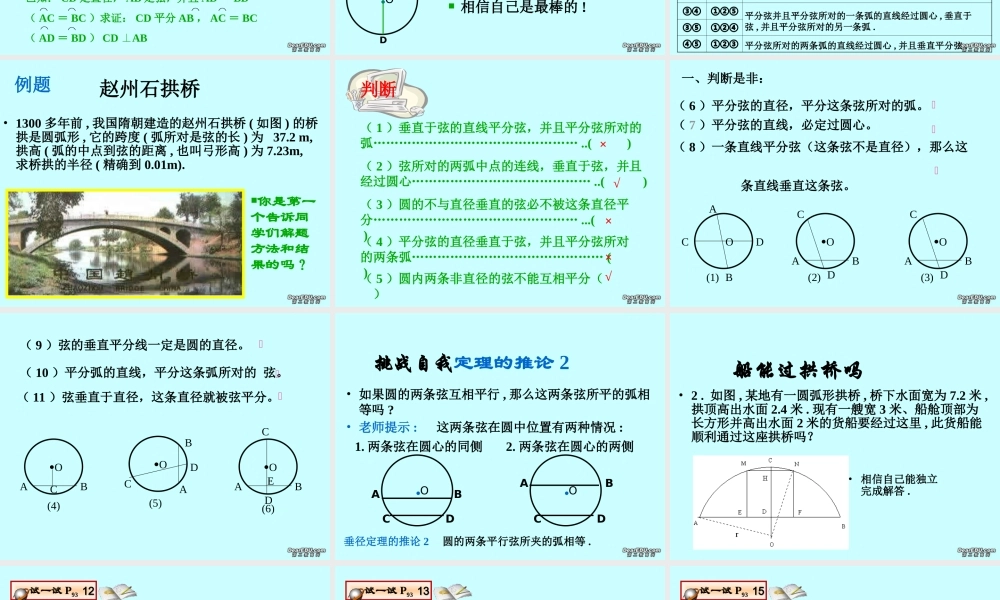
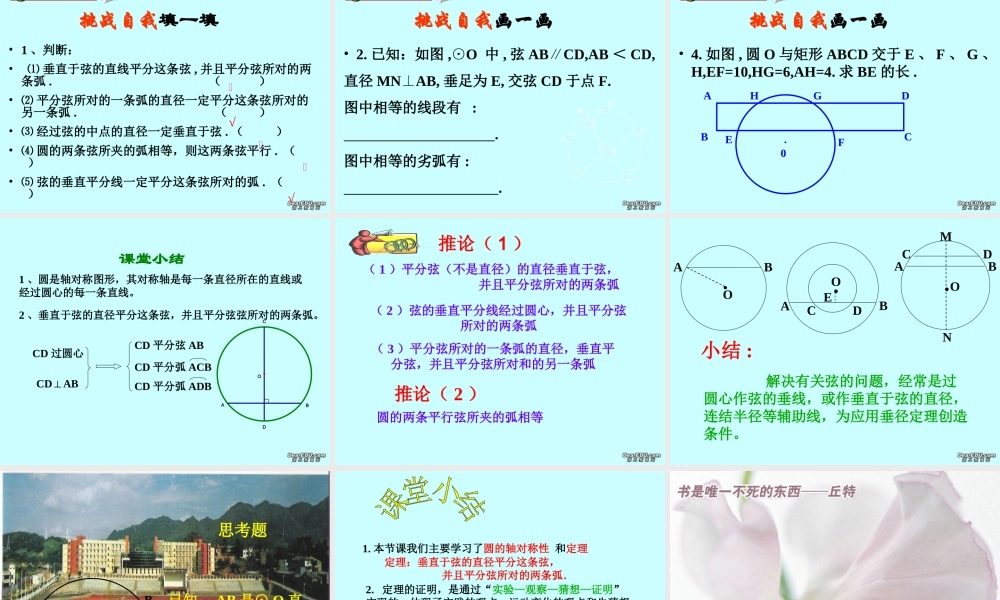
九年级数学 ( 下 ) 第三章圆 圆的对称性 (2)•定理 垂直于弦的直径平分弦 , 并且平分• 弦所对的两 条弧 .●OABCDM└CDAB,⊥如图 CD 是直径 ,∴AM=BM,⌒ ⌒ AC =BC, ⌒⌒ AD =BD.条件CD 为直径CDAB⊥CD 平分弧 ADBCD 平分弦 ABCD 平分弧 ACB结论复习②CDAB,⊥• AB 是⊙ O 的一条弦 , 且 AM=BM.• 你能发现图中有哪些等量关系 ? 与同伴说说你的想法和理由 . 过点 M 作直径 CD.●O 右图是轴对称图形吗 ? 如果是 , 其对称轴是什么 ?小明发现图中有 :CD由 ① CD 是直径 ③ AM=BM可推得⌒ ⌒④AC=BC,⌒ ⌒⑤AD=BD.● MAB┗平分弦(不是直径)的直径垂直于弦 , 并且平 分弦所对的两条弧 .探索规律讨论( 1 )过圆心 ( 2 )垂直于弦 ( 3 )平分弦 ( 4 )平分弦所对优弧 ( 5 )平分弦所对的劣弧( 3 )( 1 )( 2)( 4)( 5)( 2)( 3)( 1)( 4)( 5)( 1)( 4)( 3)( 2)( 5)( 1)( 5)( 3)( 4)( 2)( 1 )平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧( 2 )弦的垂直平分线经过圆心,并且平分弦所对的两条弧( 3 )平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧命题( 1 ):平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧已知: CD 是直径, AB 是弦,并且 CD 平分 AB求证: CDAB⊥, AD = BD , AC = BC⌒⌒⌒⌒命题( 2 ):弦的垂直平分线经过圆心,并且平分弦所对的两条弧已知: AB 是弦, CD 平分 AB ,CD AB⊥,求证: CD 是直径, AD = BD , AC = BC⌒⌒⌒⌒命题( 3 ):平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧已知: CD 是直径, AB 是弦,并且 AD = BD ( AC = BC )求证: CD 平分 AB , AC = BC( AD = BD ) CD AB ⊥⌒⌒⌒⌒⌒⌒⌒⌒.OAEBDC 你可以写出相应的命题吗 ? 相信自己是最棒的 !定理的逆定理•如图 , 根据垂径定理与推论可知对于一个圆和一条直线来说。如果在下列五个条件中 :只要具备其中两个条件 , 就可推出其余三个结论 .●OABCDM└ ① CD 是直径, ③ AM=BM, ② CDAB,⊥⌒ ⌒④AC=BC,⌒ ⌒⑤AD=BD.注意定理及逆定理●OABCDM└条件结论定理及逆定理①②③④⑤①③②④⑤①④②③⑤①⑤②③④②③...