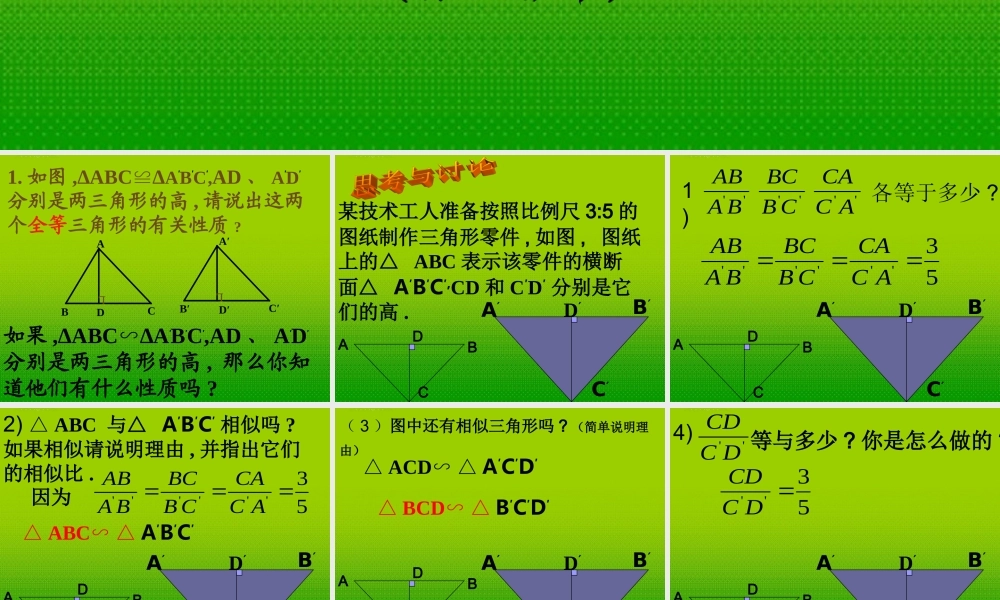
(第一课时)北师大版 八年级 下册(第四章)ⅬABCDⅬA′B′C′D′1. 如图 ,∆ABC∆≌ A′B′C′,AD 、 A′D′分别是两三角形的高 , 请说出这两个全等三角形的有关性质 ?如果 ,∆ABC∆A∽′B′C′,AD 、 A′D′分别是两三角形的高 , 那么你知道他们有什么性质吗 ? 某技术工人准备按照比例尺 3:5 的图纸制作三角形零件 , 如图 , 图纸上的△ ABC 表示该零件的横断面△ A′B′C′,CD 和 C′D′ 分别是它们的高 . ABCD A′B′C′D′ ABCD A′B′C′D′53''''''ACCACBBCBAAB''CBBC''ACCA1)各等于多少 ?''BAAB ABCD A′B′C′D′2) ABC △与△ A′B′C′ 相似吗 ?如果相似请说明理由 , 并指出它们的相似比 . 53''''''ACCACBBCBAAB因为 △ ABC ∽ △ A′B′C′ ABCDB′ A′C′D′( 3 )图中还有相似三角形吗 ? (简单说明理由) △ ACD ∽ △ A′C′D′ △ BCD ∽ △ B′C′D′ ABCD A′B′C′D′4) ''DCCD等与多少 ? 你是怎么做的 ?53''DCCD已知△ ABC ∽ △ A′B′C′ . ABC△与 △ A′B′C′ 他们的相似比为 k1) 如果 CD 和 C’D’ 是它们的对应高 ,那么 等与多少 ?''DCCD2) 如果 CE 和 C’E’ 是它们的角平分线 , 那么 等 与多少 ?''ECCE?''FCCF中位线是 CF 和 C’F’相似三角形对应高的比与相似比的关系及其理由如图 △ ABCDEF.B =E.∽△∴∠∠又 ∠ AMB =DNE =90∠0.∴△AMBDNE.∽△( 两角对应相等的两个三角形相似 ).相似三角形对应高的比等于相似比 .理由是 :( 相似三角形对应边成比例 ).ABCMDEFN.DEABDNAM 相似三角形对应角平分线的比与相似比的关系及其理由如图 △ ABCDEF.∽△∴∠B =E, BAC=EDF.∠∠∠又 AM,DN 分别是∠ BAC 和∠ EDF的角平分线 .∴∠BAM=EDN.∠∴△AMBDNE.∽△( 两角对应相等的两个三角形相似 ).相似三角形对应角平分线的比等于相似比 .理由是 :( 相似三角形对应边成比例 ).ABCM DEFN.DEABDNAM 相似三角形对应中线的比与相似比的关系及其理由如图 △ ABCDEF.∽△∴∠B =E,∠相似三角形对应中线的比等于相似比 .理由是 :( 相似三角形对应边成比例 ).ABCM DEFN.DEABDNAM .EFBCDEAB 又 AM,DN 分别是△ ABC 和△ DEF 的中线 ..EFBCENBM ∴△AMBDNE.∽△( 两边对应成比例且夹角相等的两个三角形相似 )..E...