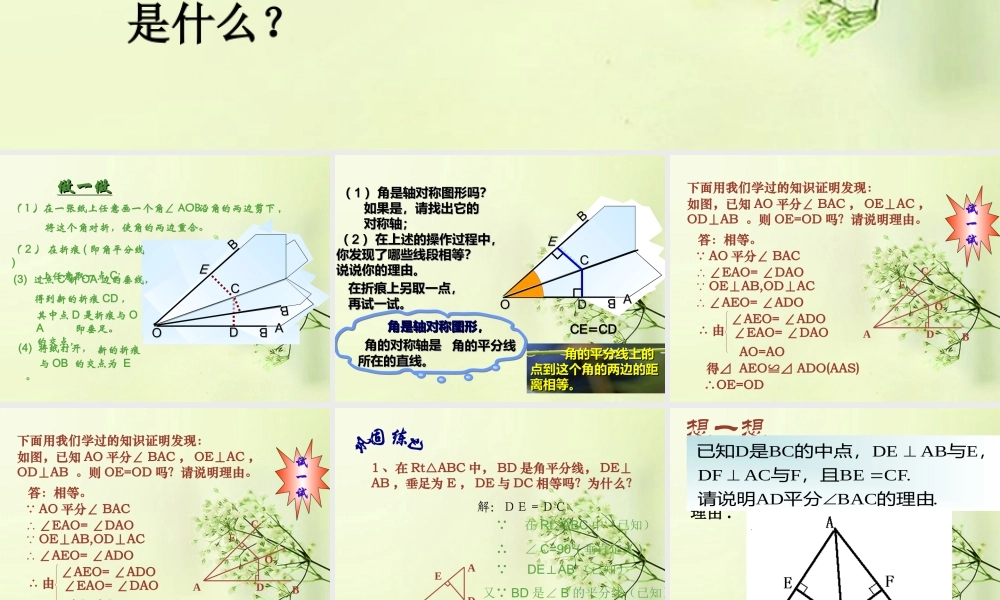
一、复习1 、什么叫轴对称图形和轴对称? 答:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。这条直线叫做对称轴。 2 、轴对称与轴对称图形的联系和区别是什么? 对于两个图形,如果沿一条直线对折后,它们能完全重合,那么称这两个图形成轴对称。这条直线就是对称轴。做一做做一做( 1 )在一张纸上任意画一个角∠ AOB AAOOBB沿角的两边剪下 ,将这个角对折,使角的两边重合。OOAA( 2 ) 在折痕 ( 即角平分线) 上任意取一点 C;(3) 过点 C 折 OA 边的垂线,得到新的折痕 CD ,其中点 D 是折痕与 OA的交点,即垂足。(4) 将纸打开,BBBBBBBBBBCCAABBAABBAA BBAA BBCCDDAA BBAA BBAABBAABBBBAACCBB 新的折痕 与 OB 的交点为 E 。BBBBBBCCEEAAOOBBBBBBBBBBBBCCAABBAABBCCDDAABBBBAACC(( 11 ))角是轴对称图形吗?角是轴对称图形吗?角是轴对称图形,角是轴对称图形,如果是,请找出它的如果是,请找出它的对称轴;对称轴;角的对称轴是角的对称轴是 角的平分线角的平分线所在的直线。所在的直线。(( 22 ))在上述的操作过程中,在上述的操作过程中,你发现了哪些线段相等?你发现了哪些线段相等?说说你的理由。说说你的理由。CECE==CDCD 角的平分线上的角的平分线上的点到这个角的两边的距点到这个角的两边的距离相等。离相等。BBCCEE在折痕上另取一点,在折痕上另取一点,再试一试。再试一试。答:相等。 AO 平分∠ BAC ∴ ∠EAO= ∠DAO OE⊥AB,OD⊥AC ∴ ∠AEO= ∠ADO∴ 由∠AEO= ∠ADO∠EAO= ∠DAOAO=AO得⊿ AEO≌⊿ ADO(AAS)∴OE=OD试一试下面用我们学过的知识证明发现:如图,已知 AO 平分∠ BAC , OE⊥AC ,OD⊥AB 。则 OE=OD 吗?请说明理由。ABCEDO答:相等。 AO 平分∠ BAC ∴ ∠EAO= ∠DAO OE⊥AB,OD⊥AC ∴ ∠AEO= ∠ADO∴ 由∠AEO= ∠ADO∠EAO= ∠DAOAO=AO得⊿ AEO≌⊿ ADO(AAS)∴OE=OD试一试下面用我们学过的知识证明发现:如图,已知 AO 平分∠ BAC , OE⊥AC ,OD⊥AB 。则 OE=OD 吗?请说明理由。ABCEDO1 、在 Rt△ABC 中, BD 是角平分线, DE⊥AB ,垂足为 E , DE 与 DC 相等吗?为什么? ABCDE解:DE=DC 在 Rt ABC⊿中(已知)∴ ∠ C=90°( 垂直定义 ) DEAB⊥(已知)又 BD 是∠ B 的平分线(已知)∴DE=DC( 角平分线的...