中考数学复习 一元二次方程课件 苏教版 课件VIP免费

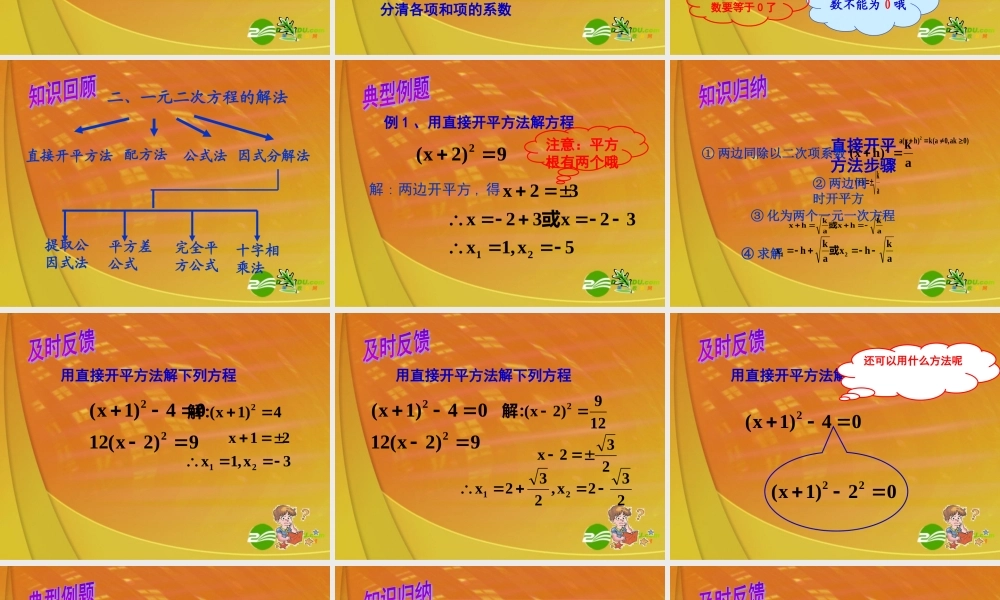
一元二次方程课题 学习目标知识回顾典型例题和及时反馈 1 、会用直接开平方法、配方法、公式法、因式分解法解简单的数字系数的一元二次方程；2 、体会转化、降次思想的应用，领会一元二次方程不同解法之间的相互联系。 一、一元二次方程的定义和一般形式 一、一元二次方程的定义和一般形式只含有 未知数，且未知数的是 的整式方程叫做一元二次方程。 0cbxax2一般形式：一个最高次数2)0a(  二次项 二次项系数 a= 一次项 一次项系数 b=常数项 c = 化成一般形式、将一元二次方程例)1x2)(2x(5x31205x3x213点评：注意化简过程中的符号变化，分清各项和项的系数2xx35 m2、当例m当时，方程时，方程是03x)2m(x)4m(22一元一次方程一元一次方程注意一次项系数不能为 0 哦2只需考虑二次项系数不等于 0 就行了2是一元二次方程03x)2m(x)4m(22这时二次项系数要等于 0 了 二、一元二次方程的解法配方法直接开平方法因式分解法公式法提取公因式法平方差公式完全平方公式十字相乘法 例 1 、用直接开平方法解方程 9)2x(2 5x,1x32x32x21或注意：平方根有两个哦解 : 两边开平方 , 得32x ③ 化为两个一元一次方程akhxakhx或)0ak,0a(k)hx(a2直接开平方法步骤akhx② 两边同时开平方④ 求解akhxakhx21或① 两边同除以二次项系数ak)hx(2  用直接开平方法解下列方程 9)2x(1204)1x(224)1x(2 解：21x3x,1x21 用直接开平方法解下列方程 9)2x(1204)1x(22129)2x(2 解：232x232x,232x21 用直接开平方法解下列方程 04)1x(2还可以用什么方法呢02)1x(22 例 2 、配方法解方程05x8x42解 : 化二次项系数为 1 ，得045x2x2移项，得45x2x2配方，得49)1x491x2x22即（21x,25x231x21 配方法步骤)0a(0cbxax2① 二次项系数化为 10acxabx2③ 两边同时加上一次项系数一半的平方222)a2b(ac)a2b(xabx④ 化为直接开平方形式222a4ac4b)a2bx(⑤ 解方程)0ac4b(a2ac4bbx22acxabx2② 移常数项到右边点评：配方法的关键是将一元二次方程化为 的 形式b)ax(2)0k(k)hx(2 用配方法解下列方程 2x8x2解：16216x8x218...