八年级数学下册 2.2.1(分式的乘除法 第1课时))课件 湘教版 课件VIP免费

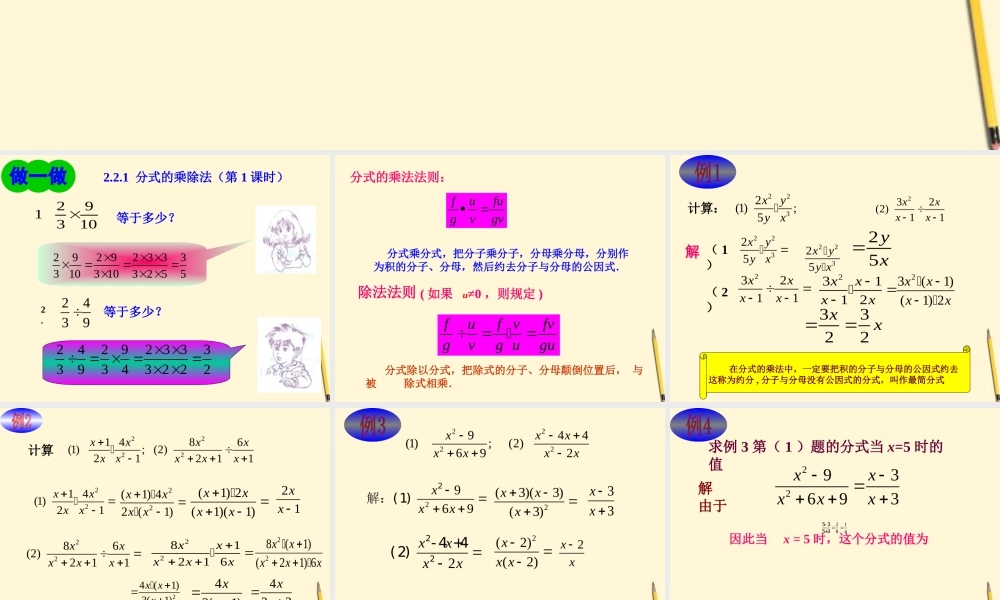
义务教育课程标准实验教科书等于多少？等于多少？243924292 3 3339343 2 22     2.2.2.1 分式的乘除法（第 1 课时）291310292 92 3 333103 103 2 55  分式的乘法法则：fufugvgvfuf vfvgvg ugu( 如果 u≠0 ，则规定 )除法法则 分式除以分式，把除式的分子、分母颠倒位置后， 与被 除式相乘． 分式乘分式，把分子乘分子，分母乘分母，分别作为积的分子、分母，然后约去分子与分母的公因式．计算：2232(1);5xyyx232(2)11xxxx22325xyy x23211xxxx23112xxxx23(1)(1) 2xxxx3322xx22325xyyx  25yx解 （ 1）（ 2） 在分式的乘法中，一定要把积的分子与分母的公因式约去这称为约分 , 分子与分母没有公因式的分式，叫作最简分式计算22221 486(1); (2)21211xxxxxxxxx(1) 2(1)(1)xxxx43(1)xx221 4(1)21xxxx22(1) 42(1)xxx x21xx 2286(2)211xxxxx2281216xxxxx 228(1)(21) 6xxxxx24(1)3(1)x xx433xx 从例 2 看到，有时需要把分子或分母中的某些多项因式分解，然后约分，化成最简分式2222944(1);(2)692xxxxxxx 把一个分式化成最简分式的好处之一， 是可以使求分式的值比较简便．2(2)(2)xx x2969xxx2解：(1)2(3)(3)(3)xxx33xx2xxxx 22-4 +4(2)2xx21845-35+3因此当 x = 5 时，这个分式的值为2293693xxxxx解 由于求例 3 第（ 1 ）题的分式当 x=5 时的值1. 计算： 222613xyyx 2382632x yxy 241312xxx   24244xxx22263xyy x4yx2381326x yxy224xy(2)(2)112xxxx21xx21(2)(2)xx12x 2. 化简： 2511025xyxyy 2222xxyyyx2(5)(5)x yy5xy2()xyyxy x • 3. 求例 3 第（ 2 ）题的分式当 x = 5 时的值355-25因此当 x = 5 时，这个分式的值为解 由于2(2)(2)xx x2xxxx 22-4 +4(2)2xx