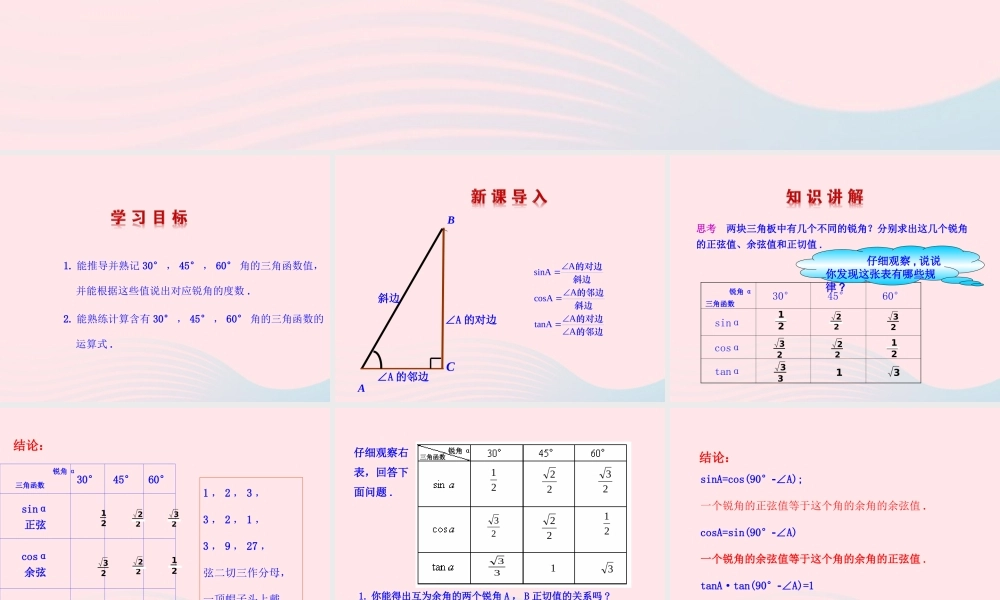
ABCcba┌28.1 锐角三角函数第 3 课时1. 能推导并熟记 30° , 45° , 60° 角的三角函数值,并能根据这些值说出对应锐角的度数 .2. 能熟练计算含有 30° , 45° , 60° 角的三角函数的运算式 . AB C∠A 的对边∠A 的邻边斜边AsinAAcosAAtanAA的对边斜边的邻边斜边的对边的邻边思考 两块三角板中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值 .30°45°60°sinαcosαtanα1222323222123313 仔细观察 , 说说你发现这张表有哪些规律 ?锐角 α三角函数30°45°60°sinα正弦cosα余弦tanα正切32739122232322212331 , 2 , 3 ,3 , 2 , 1 ,3 , 9 , 27 ,弦二切三作分母,一顶帽子头上戴 .锐角 α三角函数结论:1. 你能得出互为余角的两个锐角 A , B 正切值的关系吗 ?2. 你能得出一个锐角 A 的正弦值、余弦值和正切值的关系吗 ?2123222123223313仔细观察右表,回答下面问题 .锐角 α三角函数sinA=cos(90°∠A);一个锐角的正弦值等于这个角的余角的余弦值 .cosA=sin(90°∠A)一个锐角的余弦值等于这个角的余角的正弦值 .tanA·tan(90°∠A)=1一个锐角的正切值与这个角的余角的正切值互为倒数 .结论:【例】求下列各式的值 .(1) cos260°+sin260°. sin²60° 表示( sin60°)² ,即(sin60°)·(sin60°).【解析】( 1 ) cos 60°+sin 60°²² = ( )² + ( ) ²1232= ÷ 2222cos45tan 45sin 45 -1=0.=1.当 A , B 为锐角时,若 A≠B ,则sinA≠sinB , cosA≠cosB , tanA≠tanB.( 2 )(2)cos45 sin45 -tan45 【例题】.1. (黄冈 · 中考) cos30°= ()A .B . C . D .【解析】选 C. 由三角函数的定义知 cos30°=22323 .21232. (荆门 · 中考)计算的结果等于( )【答案】 B2sin4512A2 B 1 C D22....3. (眉山 · 中考)如图,已知梯形 ABCD 中, AD∥BC ,∠B=30° ,∠ C=60° , AD=4 , AB= ,则下底 BC 的长为__________ .60°30°DCBA3 3【答案】 10242(2cos 45sin 60 )4 232 62(2)224原式66222 24. (丹东 · 中考)计算:【解析】 ..CDBA5 .(巴中 · 中考)已知如图所示,在梯形 ABCD中, AD∥BC , AB = AD = DC = 8 ,∠ B = 60° ,...