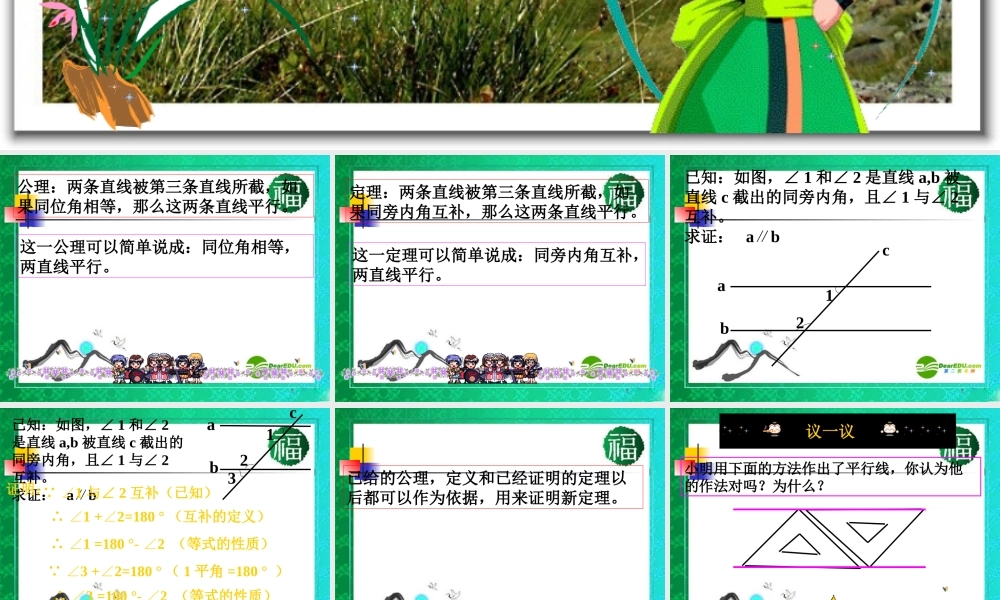
为什么它们平行 公理:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。这一公理可以简单说成:同位角相等,两直线平行。 定理:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。这一定理可以简单说成:同旁内角互补,两直线平行。 已知:如图,∠ 1 和∠ 2 是直线 a,b 被直线 c 截出的同旁内角,且∠ 1 与∠ 2互补。求证: ab∥abc12 已知:如图,∠ 1 和∠ 2是直线 a,b 被直线 c 截出的同旁内角,且∠ 1 与∠ 2互补。求证: ab∥abc123证明: ∵ ∠1 与∠ 2 互补(已知) ∴ ∠1 +2=180 °∠(互补的定义) ∴ ∠1 =180 °- 2 ∠(等式的性质) ∵ ∠3 +2=180 °∠( 1 平角 =180 ° ) ∴ ∠3 =180 °- 2 ∠(等式的性质) ∴ ∠1 =3∠ (等量代换) ∴ ab∥ (同位角相等,两直线平行) 已给的公理,定义和已经证明的定理以后都可以作为依据,用来证明新定理。 议一议小明用下面的方法作出了平行线,你认为他的作法对吗?为什么? 定理:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。这一定理可以简单说成:内错角相等,两直线平行。 已知:如图,∠ 1 和∠ 2 是直线 a,b 被直线 c 截出的内错角,且∠ 1=2∠ 。求证: ab∥abc12 已知:如图,∠ 1 和∠ 2是直线 a,b 被直线 c 截出的内错角,且∠ 1=2∠ 。求证: ab∥证明: ∵ ∠1=2 ∠(已知)∠1 +3=180 °∠( 1 平角 =180 ° ) ∴ ∠3 +2=180 °∠(等量代换) ∴ ∠2 与∠ 3 互补 (互补的定义) ∴ ab∥ (同旁内角互补,两直线平行)abc123借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论? 随堂练习蜂房的底部由三个全等的四边形围成,每个四边形的行状如图所示,其中∠ α=109 °28′ ,∠в=70°32′ 。试确定这个四边形的形状,并说明你的理由。αввα这个四边形是平行四边形。 习题 6.3证明:对顶角相等。已知:如图,直线 AB , CD 相交与点 O , ∠ 1 和∠ 2 是对顶角。求证: ∠ 1=2∠ABCDO12 习题 6.3已知:如图,直线 a , b 被直线 c 所截, 且∠ 1 +2=180 ° ∠。求证: ab∥你有几种证明方法?abc12