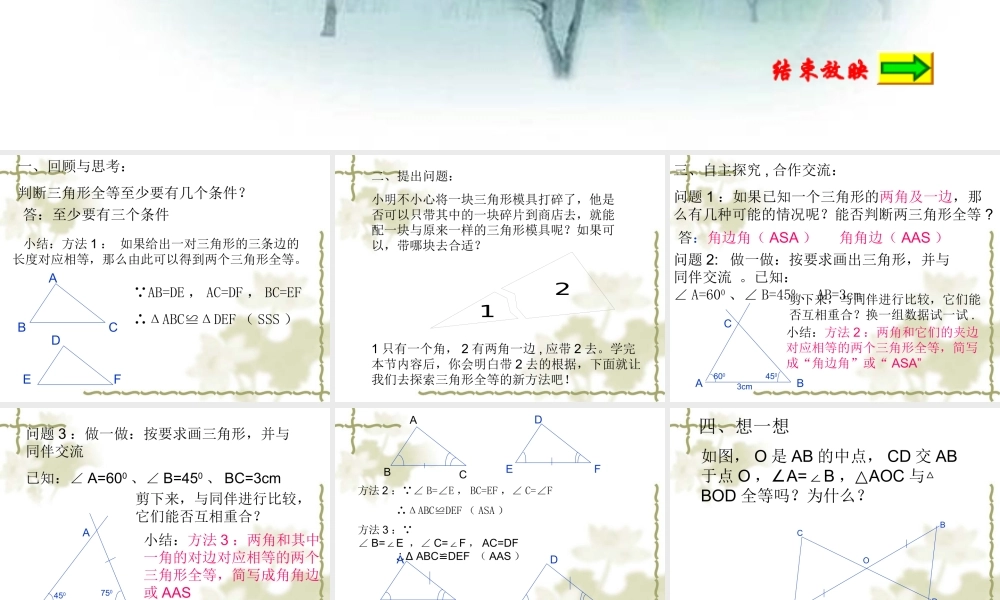
探索三角形全等的条件探索三角形全等的条件探索三角形全等的条件七年级数学下册(北师大版)结束放映 一、回顾与思考:判断三角形全等至少要有几个条件?答:至少要有三个条件 小结:方法 1 : 如果给出一对三角形的三条边的长度对应相等,那么由此可以得到两个三角形全等。ABCDEF∵AB=DE , AC=DF , BC=EF∴ΔABC≌ΔDEF ( SSS )12二、提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?1 只有一个角, 2 有两角一边 , 应带 2 去。学完本节内容后,你会明白带 2 去的根据,下面就让我们去探索三角形全等的新方法吧!三、自主探究 , 合作交流:问题 1 :如果已知一个三角形的两角及一边,那么有几种可能的情况呢?能否判断两三角形全等 ?答:角边角( ASA ) 角角边( AAS )问题 2: 做一做:按要求画出三角形,并与同伴交流 。已知:∠ A=600 、∠ B=450 、 AB=3cmABC6004503cm小结:方法 2 :两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ ASA”剪下来,与同伴进行比较,它们能否互相重合?换一组数据试一试 .问题 3 :做一做:按要求画三角形,并与同伴交流已知:∠ A=600 、∠ B=450 、 BC=3cmBCA7504503cm小结:方法 3 :两角和其中一角的对边对应相等的两个三角形全等,简写成角角边或 AAS剪下来,与同伴进行比较,它们能否互相重合?想一想 : 能否用 ASA 说明 AAS 为什么成立 ?方法 2 :∵∠ B=∠E , BC=EF ,∠ C=∠F ∴ΔABC≌DEF ( ASA )方法 3 :∵ ∠ B=∠E ,∠ C=F∠, AC=DF ∴Δ ABC≌DEF ( AAS )ABCDEFABCDEF四、想一想如图, O 是 AB 的中点, CD 交 AB于点 O ,∠A=∠B ,△AOC 与△ BOD 全等吗?为什么?ABCDO五 随堂练习:1 、如图∠ ACB=∠DFE , BC=EF ,根据 ASA 或AAS ,那么应补充一个直接条件 -------------------------- ,(写出一个即可),才能使△ ABC≌△DEF2 、如图, BE=CD ,∠ 1=2∠ ,则 AB=AC 吗?为什么?ABCDEF∠B=∠E 或∠ A=∠DCAB12ED12六、解决问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?说说你的根据七、课堂小结:1. 这堂课我们有那些收获?2. 学到现在为止我们可用几种方法说明三角形全等 ?SSS ASA AAS八、作业: P164 1 、 2 、 3