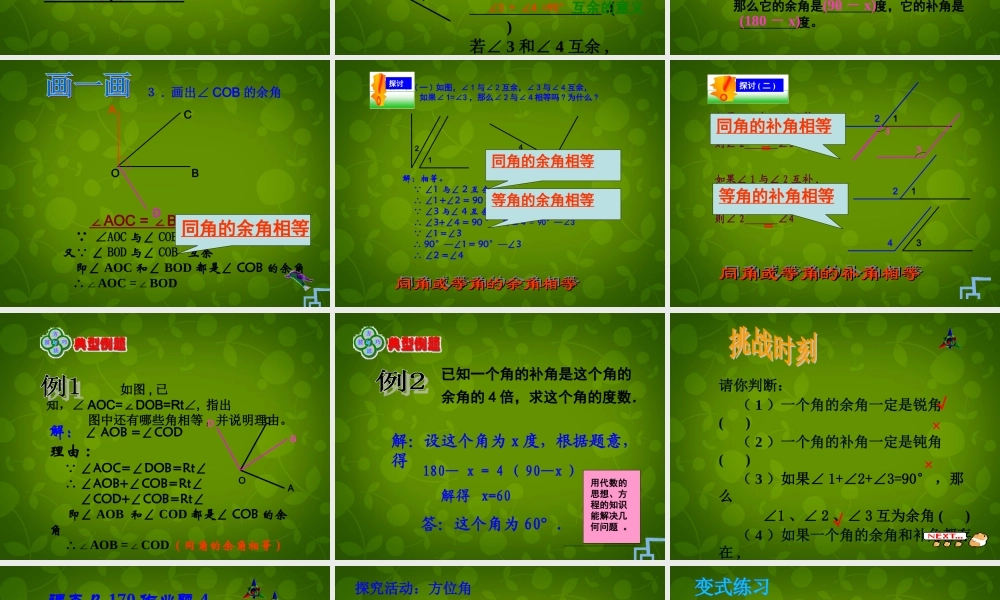
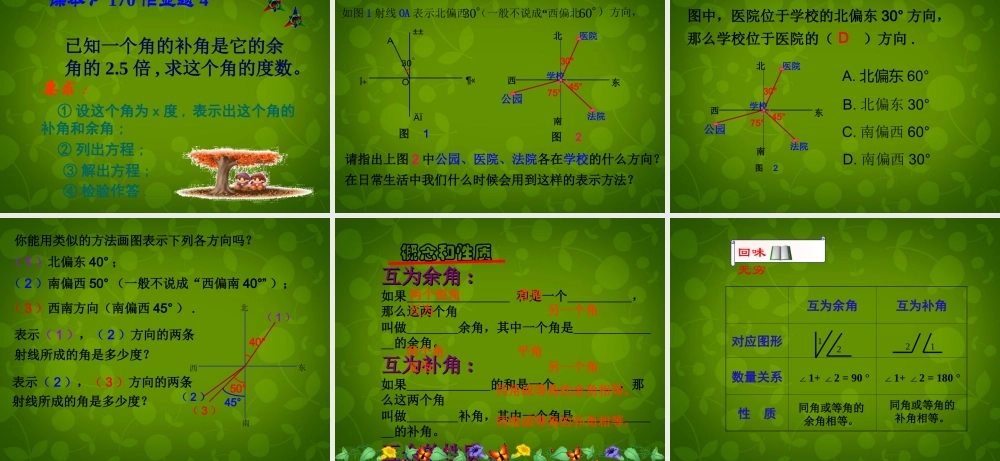
§7.6 余角和补角 角的分类锐角直角钝角平角周角90α090α180α90180α360α比较两个角的大小有两种方法 : 度量法和叠合法合作合作学习学习请你观察下图 ,∠1+∠2 与 Rt∠AOB 相等吗 ?你是怎样判断的 ?12AOB请你再观察下图 ,∠ +∠ 与平角∠ AOB相等吗 ? 你是怎样判断的 ?AOB12 如果两个锐角的和是一个直角,我们就说这两 个角互为余角,简称互余。也可以说其中一个 角是另一个角的余角 (complementary angle) 。21180°如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角 (supplementary angle) 。若∠ 1 + 2 =180 °, ∠则 .( ) 若∠ 1 和∠ 2 互补 ,则 .( )若∠ 3 + 4 =90 °,∠则 .( )若∠ 3 和∠ 4 互余 ,则 .( )3412∠1 和∠ 2 互补互补的意义∠1 + ∠2 =180°互补的意义∠3 和∠ 4 互余 互余的意义∠3 + ∠4 =90°互余的意义互余、互补的数量关系 :1. 如图 ∠ 1+∠2=90° , ⑴∠1 与∠ 2 互为 ; ⑵∠1 的余角是 ; ⑶∠1 是 的余角。余角∠2∠2122.(1)70° 角的余角是 , 它的补角是 ; (2) 如果一个角的余角是 50°12 ′ , 那么这个角的补角是 ; (3) 如果一个角为 x 度( 0° < x < 90° ), 那么它的余角是 度,它的补角是 度。20°110°140 °12 ′(90 - x)(180 - x) ∠AOC 与∠ COB 互余 又 ∠ BOD 与∠ COB 互余 即∠ AOC 和∠ BOD 都是∠ COB 的余角 ∴∠AOC =BOD ∠3 . 画出∠ COB 的余角COBAD ∠AOC = BOD∠ 同角的余角相等( 一 ) 如图,∠ 1 与∠ 2 互余,∠ 3 与∠ 4 互余, 如果∠ 1=∠3 ,那么∠ 2 与∠ 4 相等吗 ? 为什么 ?1234解:相等。 ∠1 与∠ 2 互 余 ∴ ∠1 +∠2 = 90 ° 即∠ 2 = 90°─∠1 ∠3 与∠ 4 互 余 ∴ ∠3+∠4 = 90 ° 即∠ 4 = 90°─∠3 ∠1 =∠3 ∴ 90°─∠1 = 90°─∠3 ∴ ∠2 =∠4等角的余角相等同角或等角的余角相等同角或等角的余角相等同角或等角的余角相等同角或等角的余角相等同角的余角相等探讨12 如果∠ 1 与∠ 2 互补 , ∠1 与∠ 3 互补 , 则∠ 2 ∠3= 如果∠ 1 与∠ 2 互补 , ∠3 与∠ 4 互补 , ∠1=∠3, 则∠ 2...