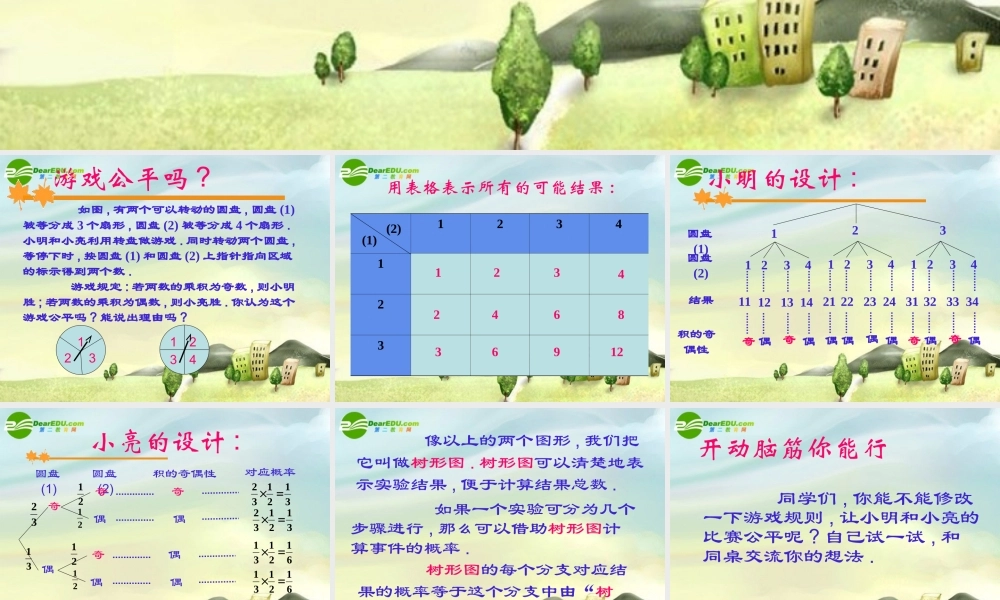
33.2 概率树形图 游戏公平吗 ? 如图 , 有两个可以转动的圆盘 , 圆盘 (1)被等分成 3 个扇形 , 圆盘 (2) 被等分成 4 个扇形 .小明和小亮利用转盘做游戏 . 同时转动两个圆盘 ,等停下时 , 按圆盘 (1) 和圆盘 (2) 上指针指向区域的标示得到两个数 . 游戏规定 : 若两数的乘积为奇数 , 则小明胜 ; 若两数的乘积为偶数 , 则小亮胜 . 你认为这个游戏公平吗 ? 能说出理由吗 ?1231234 用表格表示所有的可能结果 :1234123(2)(1)1234246836912 小明的设计 :圆盘(1)123圆盘(2)111 23422 23 24偶偶偶偶1 23432 33 34奇奇偶偶1 23412 13 14奇奇偶偶2131结果积的奇偶性 小亮的设计 :323131213221213121326121312121圆盘(1)圆盘(2)偶积的奇偶性对应概率奇偶奇奇偶偶偶奇偶612131 像以上的两个图形 , 我们把它叫做树形图 . 树形图可以清楚地表示实验结果 , 便于计算结果总数 . 如果一个实验可分为几个步骤进行 , 那么可以借助树形图计算事件的概率 . 树形图的每个分支对应结果的概率等于这个分支中由“树根”到“树梢”路径中几个事件概率的乘积 . 开动脑筋你能行 同学们 , 你能不能修改一下游戏规则 , 让小明和小亮的比赛公平呢 ? 自己试一试 , 和同桌交流你的想法 . 拓广应用 掷两枚均匀的骰子 , 得到两个点数 . 请你为“掷骰子”设计一个规则,保证游戏公平.并说明设计的合理性. 袋子中有大小一样的 3 个红球和2 个黄球 , 甲先从中任取一球 , 取后不放回 , 乙再从中任取一球 . 求两人都取到红球的概率 .继续探究若甲取后放回呢 ? 反思与评价 谈谈你学到了哪些知识?本节课有什么收获?这节课你最大的体会是什么? 作业 习题 1-3