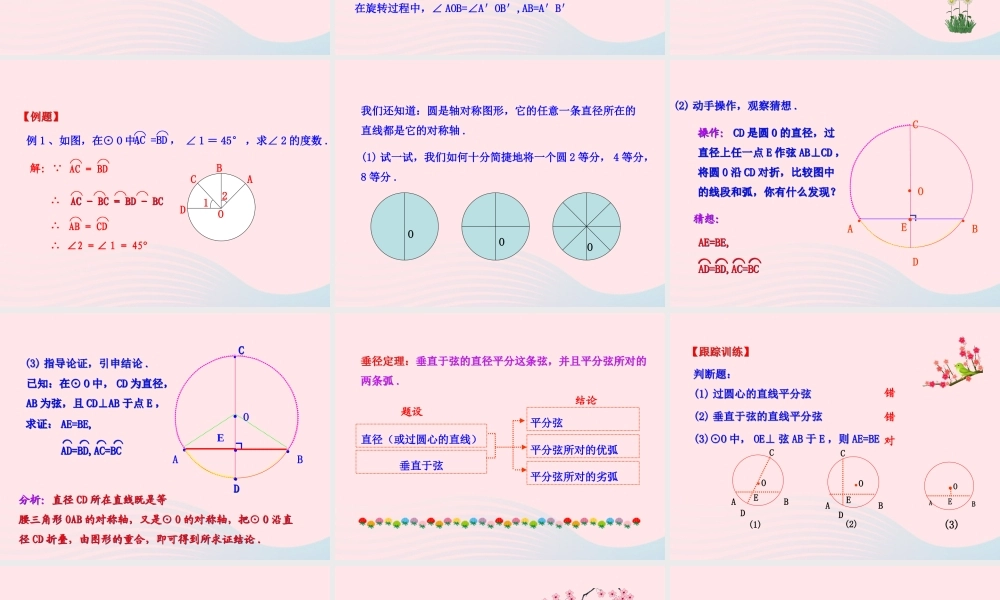
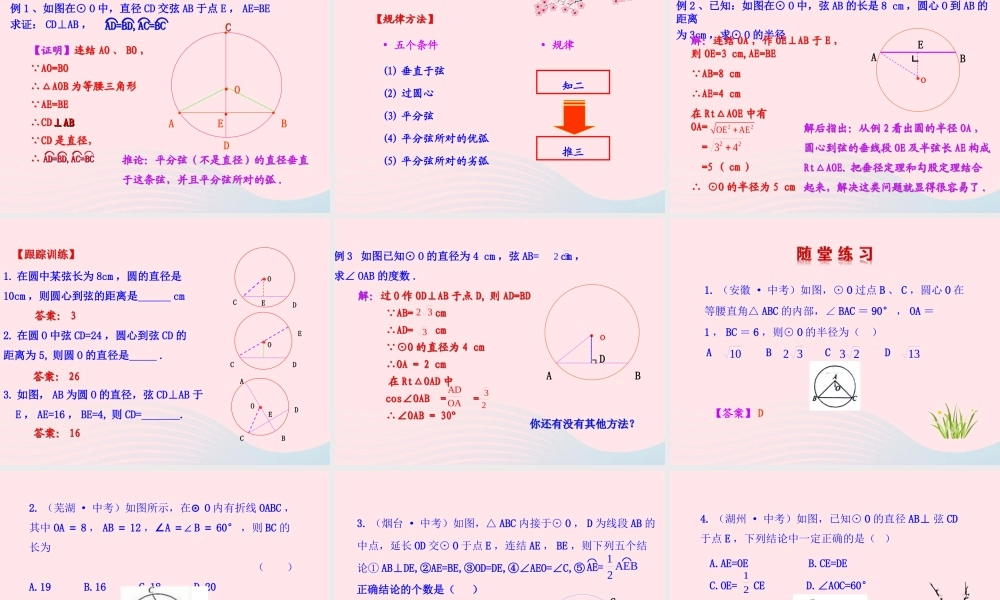
2. 圆的对称性1. 使学生知道圆是中心对称图形和轴对称图形 , 并能运用其特有的性质推出在同一个圆中 , 圆心角、弧、弦之间的关系 .2. 能运用这些关系解决问题,培养学生善于从实验中获取知识的能力 .问题:你知道赵州桥吗?它是 1 300 多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶,它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37.4 m ,拱高(弧的中点到弦的距离)为 7.2 m ,你能求出赵州桥主桥拱的半径吗?想一想:将一个圆沿着任一条直径对折,两侧半圆会有什么关系?解析:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以两侧半圆折叠后重叠 .●O利用折叠的方法即可解决上述问题 .圆也是旋转对称图形 .用旋转的方法可解决下面问题 .将图 1 中的扇形 AOB 绕点 O 逆时针旋转某个角度,画出旋转之后的图形,比较前后两个图形,你能发现什么?B′A′扇形 AOB 旋转到扇形 A′OB′ 的位置,我们可以发现,在旋转过程中,∠ AOB=∠A′OB′,AB=A′B′图 1ABO图 2ABOABA B 在一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等 .在一个圆中,如果弧相等,那么所对的圆心角相等,所对的弦相等 .在一个圆中,如果弦相等,那么所对的圆心角相等,圆心角所对的弧相等 . AB = CD∴ ⌒⌒ 解: DCOBA12例 1 、如图,在⊙ O 中, ∠ 1 = 45° ,求∠ 2 的度数 .⌒ ⌒AC =BD ,∴ ∠2 =∠ 1 = 45°⌒⌒AC = BD∴AC - BC = BD - BCAC - BC = BD - BC⌒ ⌒ ⌒ ⌒【例题】【例题】我们还知道:圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴 .(1) 试一试,我们如何十分简捷地将一个圆 2 等分, 4 等分,8 等分 .OOO(2) 动手操作,观察猜想 .(2) 动手操作,观察猜想 .操作: CD 是圆 0 的直径,过直径上任一点 E 作弦 AB⊥CD ,将圆 0 沿 CD 对折,比较图中的线段和弧,你有什么发现?操作: CD 是圆 0 的直径,过直径上任一点 E 作弦 AB⊥CD ,将圆 0 沿 CD 对折,比较图中的线段和弧,你有什么发现?猜想:猜想:AE=BE, AD=BD,AC=BCAE=BE, AD=BD,AC=BC⌒⌒ ⌒⌒ ⌒⌒⌒⌒AB•• OCDE┐•••(3) 指导论证,引申结论 .(3) 指导论证,引申结论 .求证:求证: AE=BE, AD=BD,AC=BCAE=BE, AD=BD,AC=BC⌒⌒ ⌒⌒ ⌒⌒ ⌒⌒已知:在⊙ O 中...