山西省忻州市高考数学 专题 定义域复习课件VIP免费

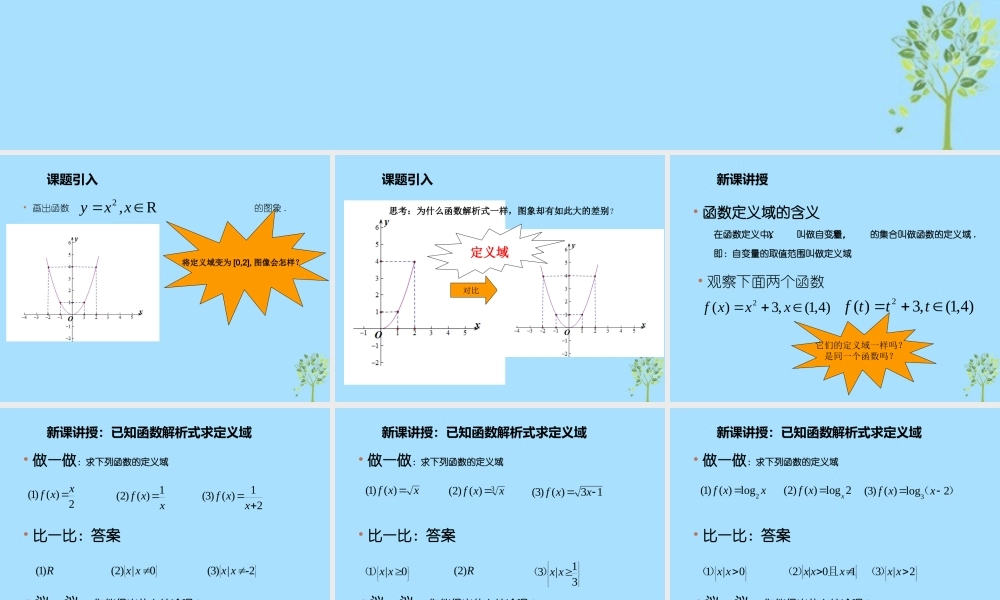
专题：求函数定义域 课题引入• 画出函数 的图象 .R2x,xy将定义域变为 [0,2], 图像会怎样？对比思考：为什么函数解析式一样，图象却有如此大的差别？课题引入定义域新课讲授• 函数定义域的含义 在函数定义中， 叫做自变量， 的集合叫做函数的定义域 . 即：自变量的取值范围叫做定义域• 观察下面两个函数)4,1(,3)(2xxxf)4,1(,3)(2tttf它们的定义域一样吗？是同一个函数吗？xx• 做一做：求下列函数的定义域新课讲授：已知函数解析式求定义域xxf1)()2(2)()1(xxf21)()3(xxf• 比一比：答案0|)2(xxR)1(2|)3(-xx• 议一议：你能得出什么结论呢？• 做一做：求下列函数的定义域新课讲授：已知函数解析式求定义域xxf)()1(3)()2(xxf13)()3(xxf• 比一比：答案01x|x）（R)2(313x|x）（• 议一议：你能得出什么结论呢？• 做一做：求下列函数的定义域新课讲授：已知函数解析式求定义域xxf2log)()1(2log)()2(xxf）（2log)()3(3xxf• 比一比：答案01x|x）（102xx|x且）（23x|x）（• 议一议：你能得出什么结论呢？此函数的定义域怎么求解呢？？？新课讲授：已知函数解析式求定义域43)1ln()(2xxxxf做一做：求此函数的定义域 .新课讲授：已知函数解析式求定义域1log)()1(2xxf443)()2(2xxxxf1)(log1)()3(22xxf• 此题，会解否？新课讲授：拓展知识.)(12)g(,)(的表达式和定义域求，已知xgfxxxxf新课讲授：总结课后作业.)4(log)1(log11log)(1222的定义域、求函数xxxxxf.、整理本专题笔记2在数学中，我们发现真理的主要工具是归纳和模拟。 —— 拉普拉斯