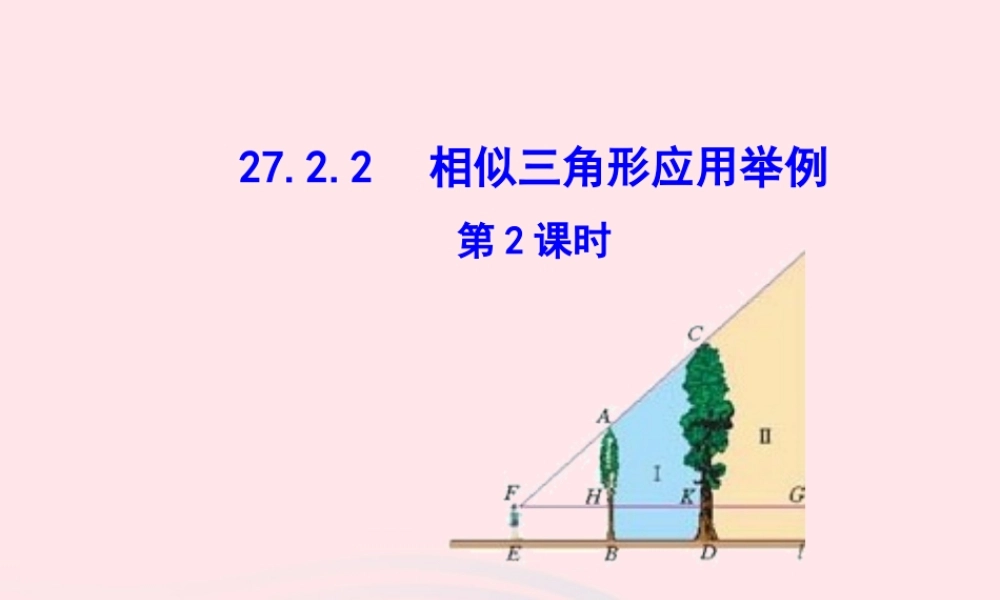
27.2.2 相似三角形应用举例第 2 课时1. 能应用相似三角形的有关知识解决一些实际问题 .2. 进一步了解数学建模的思想,培养分析问题、解决问题的能力 .基本图形归纳平行型A 型图X 型图EBCADDBCAE斜截型DABCEDABCEDABCEDABCE解决实际应用问题的关键是根据题意画出图形,或在图中找出基本图形,便于解题 .眼睛在生活中具有非常重要的作用,有它可以欣赏美丽的大好河山,有它可以辨别是非黑白,有它可以传达你对同学们的友爱……,但是你有没有想过人眼的视线在相似三角形中还有非常重要的作用 . 【例】如图左、右并排的两棵大树的高分别是 AB=8m 和 CD=12m ,两树根部的距离 BD=5m ,一个身高 1.6m 的人沿着正对这两棵树的一条水平直路 l 从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点 C ?设观察者眼晴的位置(视点)为 F ,∠ CFK 和∠ AFH 分别是观察点 C 、 A 时的仰角,区域Ⅰ和区域Ⅱ都在观察者看不到的区域(盲区)之内 .【例题】解析:假设观察者从左向右走到点 E 时,他的眼睛的位置点 F 与两棵树的顶端点 A 、 C 恰在一条直线上 .∵AB⊥l , CD⊥l ,∴AB∥CD ,△ AFH∽△CFK ,∴FHFK=AH﹕﹕CK ,即解得 FH=8.当他与左边较低的树的距离小于 8m 时,就不能看到右边较高的树的顶端点 C.FH8 1.66.4FH512 1.610.4为了测量一池塘的宽 AB, 在岸边找到了一点 C, 使 AC⊥AB ,在 AC 上找到一点 D ,在 BC 上找到一点 E, 使 DE⊥AC ,测出 AD=35m , DC=35m , DE=30m, 那么你能算出池塘的宽 AB吗 ?ABCDE【跟踪训练】解析:因为 ∠ ACB =∠ DCE,所以△ ABC∽△DEC , 答:池塘的宽 AB 为 60 m . DCACDEAB 那么 ∠CAB =∠ CDE=90°,ABCDEDEAC30 (3535)AB60()DC35解得m1. 某校宣传栏后面 2 米处种了一排树,每隔 2 米一棵,共种了 6 棵,小勇站在距宣传栏中间位置的垂直距离 3 米处,正好看到两端的树干,其余的 4 棵均被挡住,那么宣传栏的长为 ___ 米 ( 不计宣传栏的厚 ) 。3Ã×2Ã×62. (内江 · 中考)如图,为了测量某棵树的高度,小明用长为 2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点 . 此时,竹竿与这一点距离相距 6m ,与树相距 15m ,则树的高度为 _____m. 3. (德州 · 中考)如图,小明在 A 时测得某树的影长为 2m , B 时又测得该树的影长为 8m ,若两次日照的光线互相垂直,则树的高度为 _____m.A 时B 时74 在应用相似的相关知识解决实际问题时,要利用平行、垂直等辅助线构造相似三角形,将实际问题转化为相应的数学模型 .智慧的可靠标志就是能够在平凡中发现奇迹 . —— 爱默生