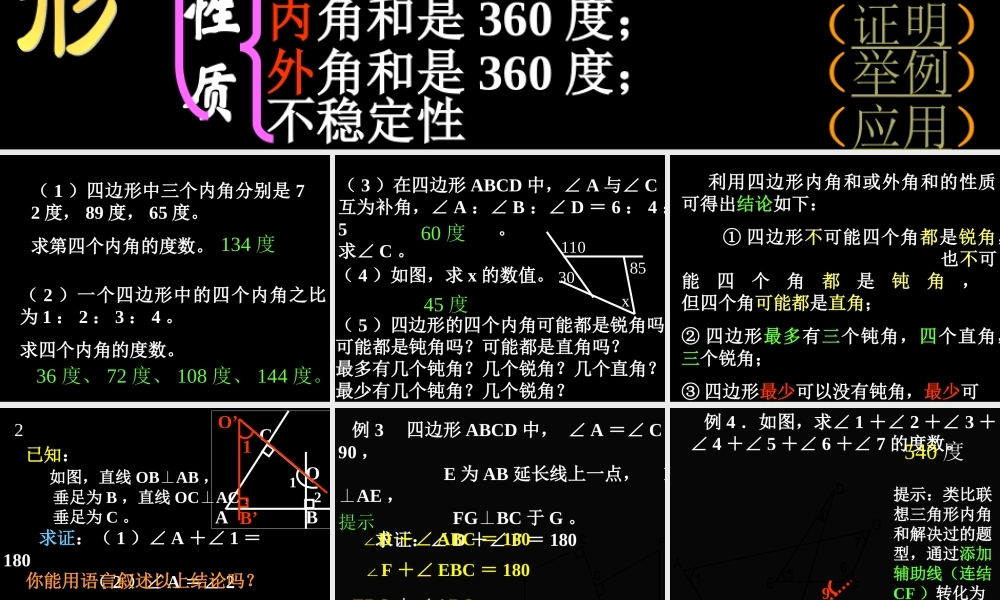
图形概念性质ABCD在平面内,定义 元素 边顶点对角线 AB 、 BC 、 CD 、 DAA 、 B 、 C 、DAC 、 BD ( 作用 )外角和是 360 度;内角和是 360 度;不稳定性(证明)(举例)(应用)由不在同一条直线上的四条线段首尾顺次相接所组成的图形叫做四边形。( 凸凹 )边的关系:较小的三边之和大于最长边( 1 )四边形中三个内角分别是 72 度, 89 度, 65 度。求第四个内角的度数。 ( 2 )一个四边形中的四个内角之比为 1 : 2 : 3 : 4 。求四个内角的度数。 134 度36 度、 72 度、 108 度、 144 度。( 3 )在四边形 ABCD 中,∠ A 与∠ C互为补角,∠ A :∠ B :∠ D = 6 : 4 :5。求∠ C 。( 4 )如图,求 x 的数值。 ( 5 )四边形的四个内角可能都是锐角吗?可能都是钝角吗?可能都是直角吗?最多有几个钝角?几个锐角?几个直角?最少有几个钝角?几个锐角? 3011085x60 度45 度 利用四边形内角和或外角和的性质可得出结论如下: ① 四边形不可能四个角都是锐角, 也不可能四个角都是钝角,但四个角可能都是直角;② 四边形最多有三个钝角,四个直角,三个锐角;③ 四边形最少可以没有钝角,最少可以没有锐角。 已知: 如图,直线 OBAB⊥, 垂足为 B ,直线 OCAC⊥, 垂足为 C 。 求证:( 1 )∠ A +∠ 1 =180 ( 2 )∠ A =∠ 2你能用语言叙述以上结论吗?(如果一个角的两边与另一个角的两边分别垂直,那么这两个角 。)ABCO12相等或互补1B’O’2 例 3 四边形 ABCD 中, ∠ A =∠ C =90 , E 为 AB 延长线上一点, EFAE⊥, FGBC⊥于 G 。 求证:∠ D +∠ F = 180GFEDCBA∠D +∠ ABC = 180∠F +∠ EBC = 180∠EBC +∠ ABC =180提示 例 4 .如图,求∠ 1 +∠ 2 +∠ 3 +∠ 4 +∠ 5 +∠ 6 +∠ 7 的度数。1234567GFEDCBA提示:类比联想三角形内角和解决过的题型,通过添加辅助线(连结CF )转化为三角形或四边形的内角和。 540 度89back四边形的不稳定性应用1. 以 AB=20mm,BC=30mm,CD=18mm,DA=21mm 为边,画四边形 ABCD.大家画出的四边形形状一样吗?请说明原因。不一样说明四边形有不稳定性ABCD20mm30mm18mm21mm画法:1. 画任意小于平角的角 B.2. 在角 B 的两边上分别截取BA=20mm,BC=30mm.3. 分别以点 A 、 C 为圆心,以 21mm 、 18mm 为半径画弧,两弧相交于点 D.4. 连结 AD 、 CD 。小结性质外角和是 360 度;内角和是 360 度;不稳定性边的关系:较小的三边之和大于最长边9 种证明方法取决于点的不同位置的选取