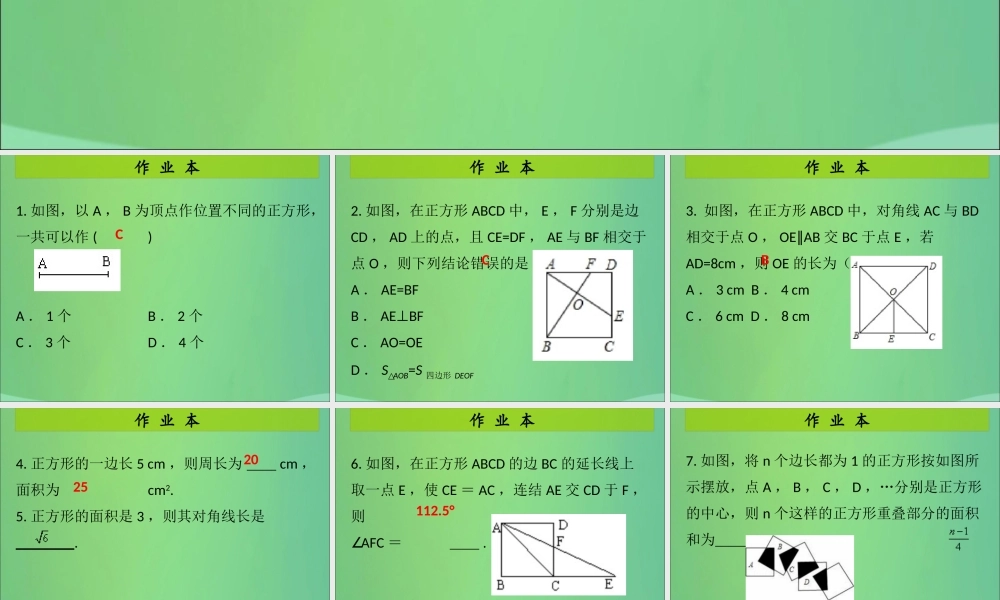
作 业 本第 7 课时 正方形的性质与判定( 1 )第一章 特殊的平行四边形作 业 本1. 如图,以 A , B 为顶点作位置不同的正方形,一共可以作 ()A . 1 个B . 2 个C . 3 个D . 4 个C作 业 本2. 如图,在正方形 ABCD 中, E , F 分别是边CD , AD 上的点,且 CE=DF , AE 与 BF 相交于点 O ,则下列结论错误的是( )A . AE=BF B . AEBF ⊥C . AO=OE D . S△AOB=S 四边形 DEOF C作 业 本3. 如图,在正方形 ABCD 中,对角线 AC 与 BD相交于点 O , OE AB∥交 BC 于点 E ,若AD=8cm ,则 OE 的长为( )A . 3 cm B . 4 cm C . 6 cm D . 8 cmB作 业 本4. 正方形的一边长 5 cm ,则周长为 cm ,面积为cm2.5. 正方形的面积是 3 ,则其对角线长是________.2025作 业 本6. 如图,在正方形 ABCD 的边 BC 的延长线上取一点 E ,使 CE = AC ,连结 AE 交 CD 于 F ,则∠AFC = .112.5°作 业 本7. 如图,将 n 个边长都为 1 的正方形按如图所示摆放,点 A , B , C , D ,…分别是正方形的中心,则 n 个这样的正方形重叠部分的面积和为 .作 业 本二、解答题(每题 30 分,共 30 分)8. 如图,在正方形 ABCD 中, P 为 BC 上一点,Q 为 CD 上一点,若∠ PAQ=45°, 求证:PQ=BP+DQ.证明:延长 QD 至 P' 使得 DP'=BP,连接 AP'.∵ 四边形 ABCD 是正方形 ,∴∠B=ADC=ADP'=90°,∠∠AB=AD,又已作 P'D=BPABPADP'∴△≌△,则∠ BAP=DAP'.∠作 业 本∵∠QAP=45°, 则∠ DAQ+PAB=45°,∠有∠ PAB=DAP'∠,∴∠ P'AD+DAQ=45°.∠P'AQ=QAP=45°,AQ=AQ,P'A=PA∵∠∠,∴△ QAPP'AQ≌△,∴ P'Q=QP.又∵ P'Q=P'D+DQ , P'D=PB ,∴ QP=DQ+BP.