九年级数学上册 平行线分三角形两边成比例 课件 北京课改版 课件VIP免费

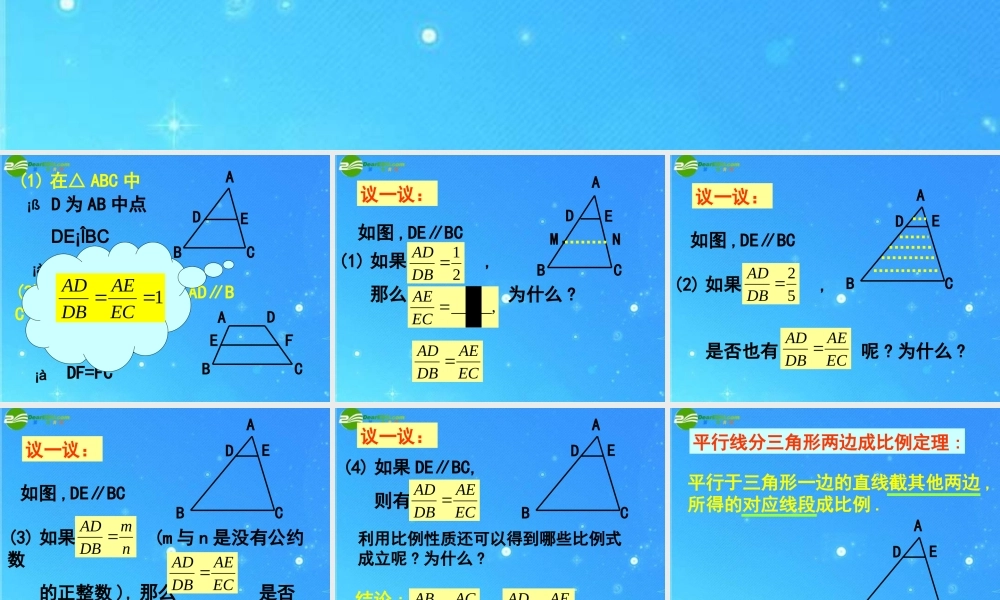
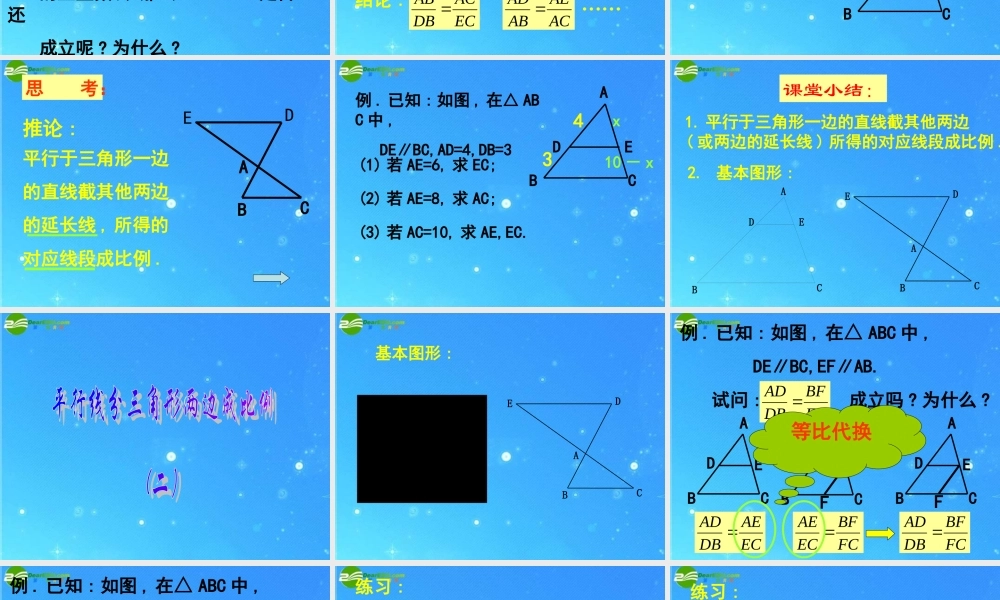
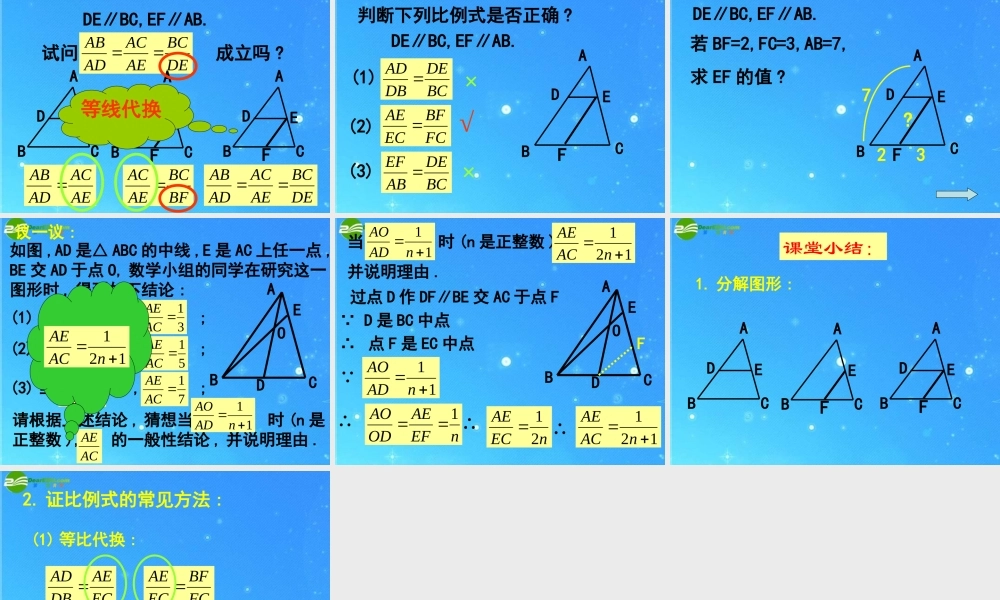
DE¡ÎBC(1) 在△ ABC 中¡ß D 为 AB 中点¡àAE=EC(2) 在梯形 ABCD 中 , AD∥BC ¡ß E 为 AB 中点¡àDF=FCABCDEFEF∥AD∥BCABCDE1ECAEDBAD 议一议：如图 ,DE∥BCABCDE(1) 如果 , 那么 为什么 ? 21DBAD_____,ECAEECAEDBAD 21NM 议一议：如图 ,DE∥BCABCDE(2) 如果 , 是否也有 呢 ? 为什么 ? 52DBADECAEDBAD  议一议：如图 ,DE∥BCABCDE(3) 如果 (m 与 n 是没有公约数 的正整数 ), 那么 是否还 成立呢 ? 为什么 ? nmDBAD ECAEDBAD  议一议：ABCDE(4) 如果 DE∥BC, 则有 ECAEDBAD 结论 :ACAEABAD ECACDBAB ……利用比例性质还可以得到哪些比例式成立呢 ? 为什么 ? 平行线分三角形两边成比例定理 :平行于三角形一边的直线截其他两边 ,所得的对应线段成比例 .ABCDE 思 考：ABCED推论 :平行于三角形一边的直线截其他两边的延长线 , 所得的对应线段成比例 . 例 . 已知 : 如图 , 在△ ABC 中 , DE∥BC,AD=4,DB=3(1) 若 AE=6, 求 EC;(2) 若 AE=8, 求 AC;(3) 若 AC=10, 求 AE,EC.ABCDE43x10 － x 课堂小结：ABCDEABCED2. 基本图形 :1. 平行于三角形一边的直线截其他两边( 或两边的延长线 ) 所得的对应线段成比例 . ABCDEABCED 基本图形 : 例 . 已知 : 如图 , 在△ ABC 中 , DE∥BC,EF∥AB. 试问 : 成立吗 ? 为什么 ?FCBFDBAD ABCDEFABCEFABCDEECAEDBAD FCBFECAE FCBFDBAD 等比代换 例 . 已知 : 如图 , 在△ ABC 中 , DE∥BC,EF∥AB. 试问 : 成立吗 ?DEBCAEACADABABCDEFABCEFABCDEAEACADAB BFBCAEAC DEBCAEACADAB等线代换 练习 :判断下列比例式是否正确 ?DE∥BC,EF∥AB.(1)BCDEDBAD (2)FCBFECAE (3)BCDEABEF ABCDEF××√ 练习 :DE∥BC,EF∥AB.ABCDEF若 BF=2,FC=3,AB=7,求 EF 的值 ?23?7 议一议 :如图 ,AD 是△ ABC 的中线 ,E 是 AC 上任一点 ,BE 交 AD 于点 O, 数学小组的同学在研究这一图形时 , 得到如下结论 :(2) 当 时 , ;51ACAE31ADAO(1) 当 时 , ;21ADAO31ACAE请根据上述结论 , 猜想当 时 (n 是正整数 ), 的一般性结论 , 并说明理由 .ACAE11nADAO(3) 当 时 , ;41ADAO71ACAEABCDEO121 nACAE ABCDEO过点 D 作 DF∥BE 交 AC 于点 F∵ D 是 BC 中点∴ 点 F 是 EC 中点∵11nADAOnEFAEODAO1∴nECAE21∴121 nACAE∴F当 时 (n 是正整数 ), 并说明理由 .11nADAO121 nACAE ABCDEFABCEFABCDE课堂小结：1. 分解图形 : ECAEDBAD FCBFECAE (1) 等比代换 :(2) 等线代换 :2. 证比例式的常见方法 :FCBFDBAD 