八年级数学平方差公式课件 华师版 课件VIP免费

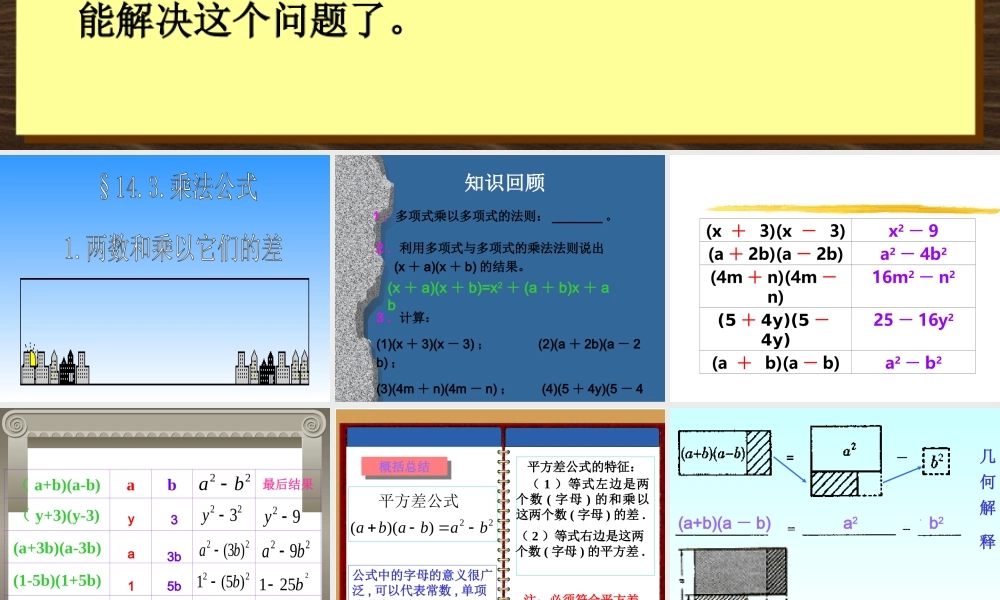
王剑同学去商店买了单价是 9.8 元／千克的糖块 10.2 千克，售货员刚拿起计算器，王剑就说出应付 99.96 元，结果与售货员计算出的结果相吻合。售货员惊讶地问：“这位同学，你怎么算得这么快 ?” 王剑同学说：“我利用了在数学上刚学过的一个公式。”你知道王剑同学用的是一个什么样的公式吗 ? 你现在能算出来吗 ? 学了本节之后，你就能解决这个问题了。 知识回顾 3 ．计算：(1)(x ＋ 3)(x － 3) ； (2)(a ＋ 2b)(a － 2b) ；(3)(4m ＋ n)(4m － n) ； (4)(5 ＋ 4y)(5 － 4y) 。1 ．多项式乘以多项式的法则： _______ 。2 ．利用多项式与多项式的乘法法则说出 (x ＋ a)(x ＋ b) 的结果。(x ＋ a)(x ＋ b)=x2 ＋ (a ＋ b)x ＋ ab (x ＋ 3)(x － 3)x2 － 9(a ＋ 2b)(a － 2b)a2 － 4b2(4m ＋ n)(4m －n)16m2 － n2(5 ＋ 4y)(5 －4y)25 － 16y2(a ＋ b)(a － b)a2 － b2 （ a+b)(a-b)ab最后结果（ y+3)(y-3)(a+3b)(a-3b)(1-5b)(1+5b)(-x+2)(-x-2)22ba y3223y92 ya3b22)3( ba 229ba 15b22)5(1b2251b－ x222 2)( x42 x概括总结概括总结22)()( bababa平方差公式（ 2 ）等式右边是这两个数 ( 字母 ) 的平方差 .平方差公式的特征： （ 1 ）等式左边是两个数 ( 字母 ) 的和乘以这两个数 ( 字母 ) 的差 .注：必须符合平方差公式特征的代数式才能用平方差公式公式中的字母的意义很广泛 , 可以代表常数 , 单项式或多项式 =－(a+b)(a － b)a2b2几 何 解 释例 1 计算(x+3)(x-3)=(2a+3b)(2a-3b)=223x92 x22)3()2(ba2294ba  (-3+2a)(-2a-3)22)2()3(a249a练习：课本第 82 页练习第 1 题 226)3)(2)(5(yxyxyx22))()(1(bababa22))()(2(bababa19)13)(13)(4(2 xxx( )( )×( )×××判断下列各式是否正确，并说明理由204.025.0)2.05.0)(2.05.0)(3(xxx( )( )√例 2 计算 1998 20021998  2002 =（ 2000-2 ）（ 2000+2）2222000 =4000000-4=3999996解练习： 课本第 82 页练习第 2 题例 3 街心花园有一块边长为 a 米的正方形草坪，经统 一规 划后，南北向要加长 2 米，而东西向要缩短 2 米，问改造后的长方形草坪的面积是多少？解)2)(2(aa42 a平方米面积是改造后的长方形草坪的答)4(a:2 练习：课本第 82 页练习的第 3 题。