函数的极限一 无穷极限 新课标 人教版 课件VIP免费

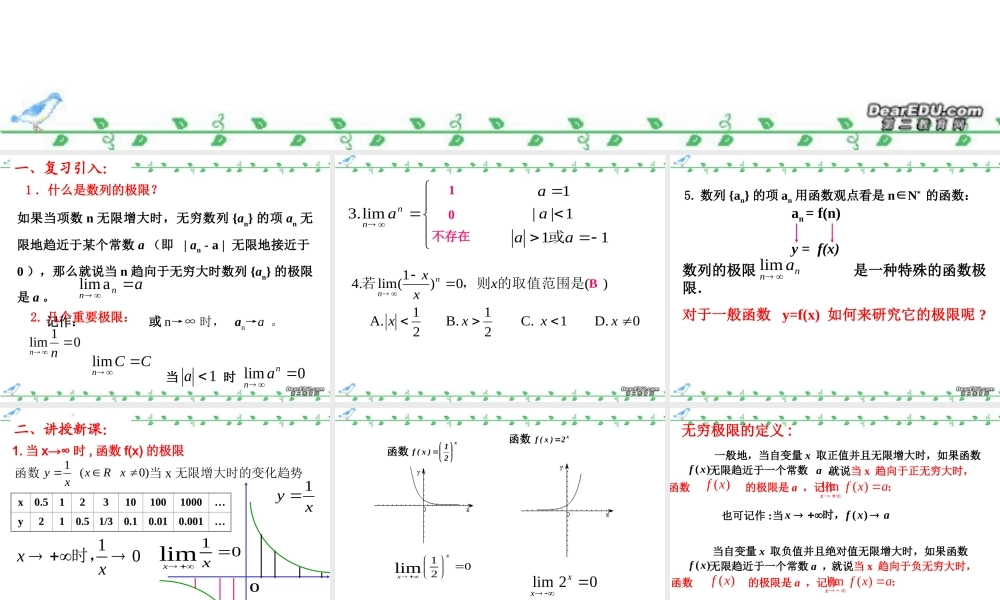
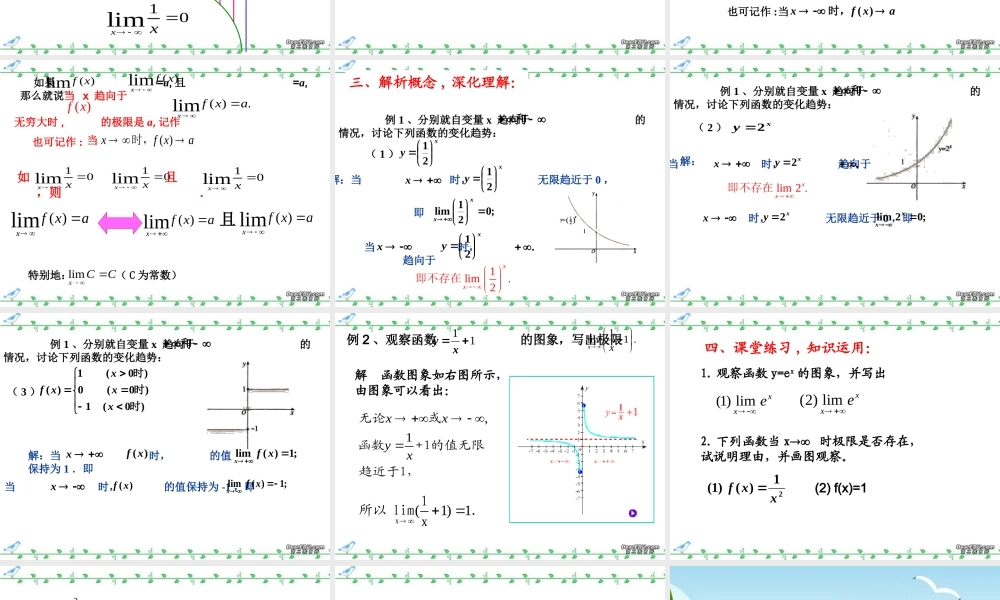
2.3 2.3 函数的极限函数的极限 (1)(1) xf x 当时函数的极限无穷极限一、复习引入： 如果当项数 n 无限增大时，无穷数列 {an} 的项 an 无限地趋近于某个常数 a （即 | an - a | 无限地接近于0 ），那么就说当 n 趋向于无穷大时数列 {an} 的极限是 a 。 记作： 或 n→∞ 时， an→a 。 ann alim1 ．什么是数列的极限？CCnlim当 时 1a0limnna2. 几个重要极限： 01lim nn11 1|| 1 lim.3aaaaann或 10不存在0 D. 1 C. 21 B. 21 A. ) (0)1(lim.4xxxxxxxnn的取值范围是，则若B5. 数列 {an} 的项 an 用函数观点看是 n∈N* 的函数： 数列的极限 是一种特殊的函数极限．对于一般函数 y=f(x) 如何来研究它的极限呢 ? nnalimy = f(x)an = f(n) 函数 当 x 无限增大时的变化趋势 )0(1xRxxy10limxx 1. 当 x→∞ 时 , 函数 f(x) 的极限二、讲授新课： 10xx 时，Oxy1x0.5123101001000…y210.51/30.10.010.001…10limxx  函数x21)x(f102limxx 函数x2)x(f02limxx就说当 x 趋向于正无穷大时，函数 的极限是 a ，记作lim( )xf xa  ；( )f x一般地，当自变量 x 取正值并且无限增大时，如果函数)(xf无限趋近于一个常数 a ，也可记作 :当axfx)(时，当也可记作 :axfx)(时，就说当 x 趋向于负无穷大时，函数 的极限是 a ，记作lim( )xf xa   ；当自变量 x 取负值并且绝对值无限增大时，如果函数)(xf无限趋近于一个常数 a ， ( )f x无穷极限的定义 :也可记作 : 当axfx)(时，CCxlim特别地： （ C 为常数）( ).limxf xa ( )limxf x ( )limxf x   如果 =a, 且 =a, 那么就说当 x 趋向于无穷大时 , 的极限是 a, 记作 ( )f x10limxx 10limxx  如 且 ，则 .10limxx ( )limxf xa ( )limxf xa  ( )limxf xa  且 例 1 、分别就自变量 x 趋向于 的情况，讨论下列函数的变化趋势：和（ 1 ）xy 21解：当 时， 无限趋近于 0 ，xy 21;021limxx即...