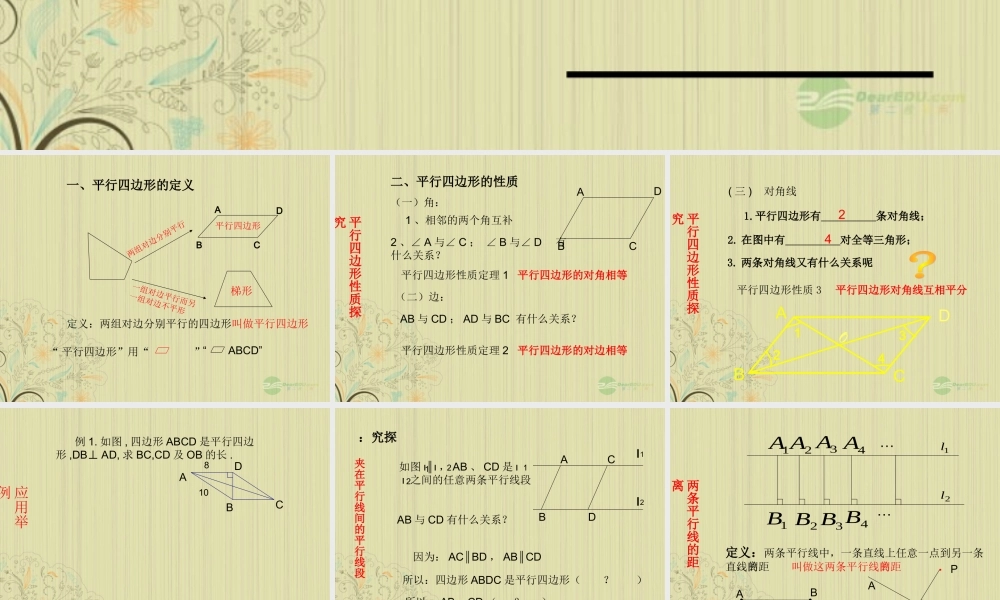
平行四边形的定义及性质两组对边分别平行一组对边平行而另一组对边不平形平行四边形梯形一、平行四边形的定义定义:两组对边分别平行的四边形叫做平行四边形ABCD“ 平行四边形”用“ ”“ ABCD”平行四边形性质探究ABCD(一)角:1 、相邻的两个角互补2 、∠ A 与∠ C ; ∠ B 与∠ D有什么关系?平行四边形性质定理 1 平行四边形的对角相等(二)边:AB 与 CD ; AD 与 BC 有什么关系?平行四边形性质定理 2 平行四边形的对边相等二、平行四边形的性质 1. 平行四边形有 条对角线;2. 在图中有 对全等三角形;3. 两条对角线又有什么关系呢O123ABD4C( 三 ) 对角线平行四边形性质探究24平行四边形性质 3 平行四边形对角线互相平分应用举例 例 1. 如图 , 四边形 ABCD 是平行四边形 ,DB⊥ AD, 求 BC,CD 及 OB 的长 .DABC810探究:ι1ι2ABCD如图 ι ι∥ , AB 、 CD 是 ι ι 之间的任意两条平行线段1212AB 与 CD 有什么关系?因为: AC BD∥, AB CD∥所以:四边形 ABDC 是平行四边形( ? )所以: AB = CD ( ? )推论: 夹在两条平行线间的平行线段相等夹在平行线间的平行线段两条平行线的距离2l1l1A2A3A4A1B2B3B4B……定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线的距离AB两点间的距离点到直线的距离· PABM例 2 如图 A′B′ BA∥, B′C′ CB∥, C′A′ AC.∥求证:①∠ ABC=B′∠, ∠ CAB=A′∠, ∠ BCA=C′∠ ②△ABC 的顶点分别是△ B′C′ A′ 各边的中点 .ABCA′B′C′证明:① A′B′ BA∥, B′C′ CB∥∴ 四边形 ABCB′ 是平行四边形 ∴ ∠ABC=B′∠( ? )同理∠ CAB=A′∠, ∠ BCA=C′∠② 由①证得四边形 ABCB′ 是平行四边形同理 四边形 ACBC′ 是平行四边形 ∴ AB′=BC , AC′=BC , ( ? ) ∴ AB′= AC′ 同理 BC′= BA′ CB′= CA′ ∴ △ABC 的顶点分别是△ B′C′ A′ 各边的中点应用举例3. 如图: ABCD 的周长为 36 , AB=8 , BC= ;当∠ B=60° 时 AD 、 BC 的距离AE , ABCD 的面积SABCD = .课堂练习1. 如图: ABCD 中∠ A=50° , AB=a , BC=b.则:∠ B= ,∠ C= , ABCD 的周长 = .2. 如图: ABCD 中∠ A+C=200°.∠则:∠ A= ,∠ B= .130°50°100°80°10ABCDE343402 ( a+...