八年级数学下册：重心 课件 新人教版 课件VIP免费

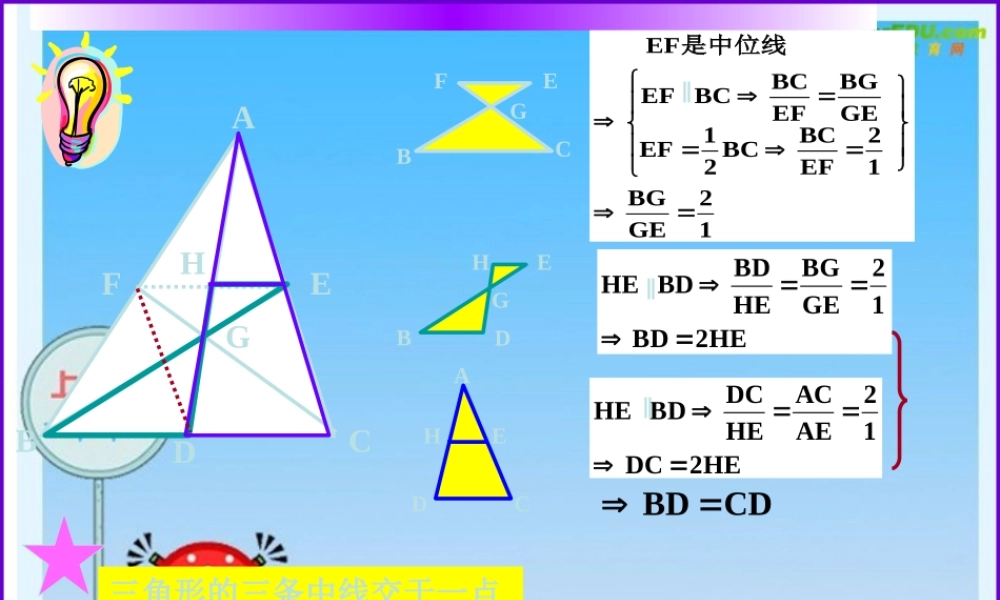
ABCFED三角形的三条中线交于一点H三角形的三条中线的交点叫做三角形的重心。GGCEFBEHGDB12GEBG12EFBCBC21EFGEBGEFBCBCEFEF是中位线‖HE2BD12GEBGHEBDBDHE‖HE2DC12AEACHEDCBDHE‖CDBD AEHCD 三角形的重心定理CBADEGF3:2:1AD:AG:GD12GECGGFBGGDAGABCG的重心是 三角形的重心与顶点的距离等于它与对边中点距离的两倍。 寻找三角形的重心ACBCBDADGDBCAGG’M DBCAGM归纳3:2:1AD:AG:DG6:3:2:1BC:DC:MC:DM3:1AC:GM关于线段：关于面积：k 2k6k6k3k…… 判断题2 、三角形的重心到一边的距离等于这边上中线长的三分之一。FEGACDB1 、等边三角形三条高的交点就是它的重心。 三角形的重心到一边中点的距离等于这边上中线长的三分之一。 三角形的重心到一边的距离等于这边上高的三分之一。DGBCA;ABCG,3BC,4AC,90ACB,ACBRto的重心是已知：求： 1. 点 G 到直角顶点 C 的距离GC ；2. 点 G 到斜边 AB 的距离FE的重心是 ABCG CD32CGCD是中线o90ACB,ACBRt解：3BC,4AC5AB 25CD 35CG  DEBCAG的长。求：相交于点中线与中已知：BC,cm5GE,cm18AD;GBEAD,BCAD,ACABABC? CDEBA;GBECDABC相交于点、的中线已知;BGCDGES:S.1求：G;DGBDGES:S.2G;EGCDGBS:S.3G;ADCDGES:S.5G;ABCDGES:S.6G;DECDGES:S.4G CBADEGF归纳有关三角形面积解题方法：1. 相似三角形面积之比等于相似比的平方；2. 等底或同底的两个三角形面积之比等于高之比；3. 等高或同高的两个三角形面积之比等于底之比。2. 要灵活应用三角形的重心定理进行计算或证明。1. 三角形的重心定理 : 三角形的重心与顶点的距离等于它与对边中点的距离的两倍。3:2:1AD:AG:GD12GECGGFBGGDAGABCG的重心是小结ABD MCGGAEFCDB3:2:1DC:MC:DMACGMABCG的重心是‖GAEFCB3. 掌握常用的数学解题方法。如利用比例线段证线段相等以及有关面积的解题方法GAEFCBD EDGMNGS:SCDNBEMGCDBEABC求中点，为中点，为若点，交于与中线中，中线思考：现在，轮到我来考你们了！MNCBADEG 这节课就上到这，回去后好好复习！