七年级数学整式的乘除和因式分解课件人教版 课件VIP免费

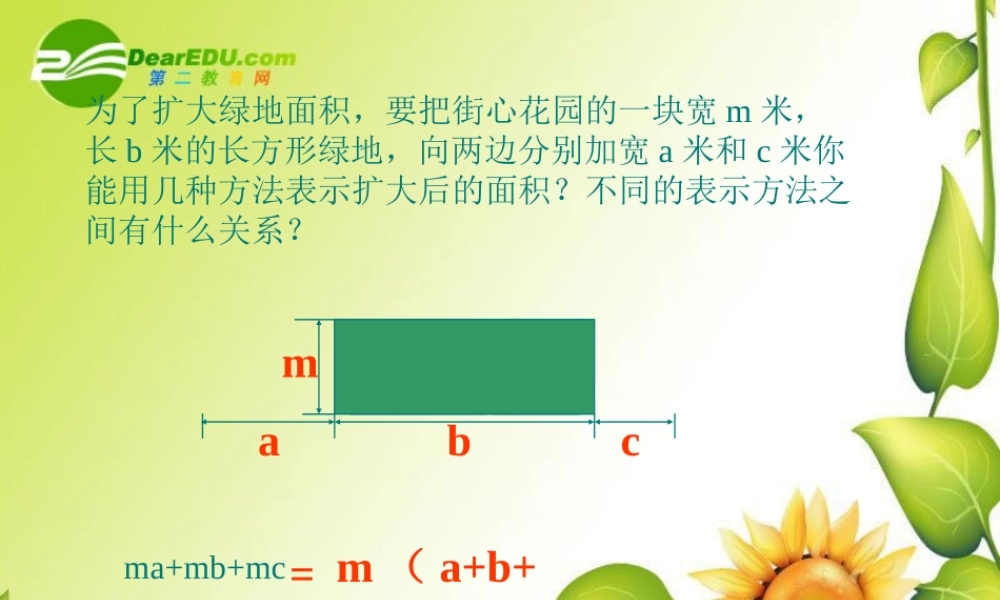
为了扩大绿地面积，要把街心花园的一块宽 m 米，长 b 米的长方形绿地，向两边分别加宽 a 米和 c 米你能用几种方法表示扩大后的面积？不同的表示方法之间有什么关系？ma+mb+mcm （ a+b+c ）=bmac 整式的乘除和因式分解 问题 一种电子计算机每秒可进行 次运算，它工作 秒可进行多少次运算？1410310 它工作 秒可进行的运算次数是 ， 310314 1010 同底数幂的乘法 我们观察 可以 发现， 和 这两个因数底数相同，是同底的幂的形式 所以我们把 这种运算叫做314 1010 1410310314 1010  根据乘方的意义填空，看看计算结果有什么规律： 222)1(25 aaa 23（ 2 ）（ 3 ） （ m ， n都是正整数）．nm55 )(5nm７５ nmnmaaa（ m ， n 都是正整数）．即同底数幂相乘，底数 ，指数 ．不变一般地，我们有［同底数幂的乘法法则］相加 当三个或三个以上同底数幂相乘时，也具有这一性质 . 用公式表示为 :如 am·an·ap = am+n+p （ m 、 n 、 p 都 是 正 整数） 例１计算：52 xx ⑴34222(2)解： 52 xx3422211)3( mmyyy11)3( mmyyy)1()1(1mmy111mmy12my（ 1)52x7x（ 2)34128253)2()2)(4(53)2()2)(4(53)2(8)2(82 练习下面的计算对不对？如果不对，怎样改正？（ 1 ） b5 · b5= 2b5 （ ） （ 2 ） b5 + b5 = b10 （ ）（ 3 ） x5 ·x5 = x25 ( ) （ 4 ） y5 · y5 = 2y10 ( )（ 5 ） c · c3 = c3 ( ) b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 · y5 =y10 c · c3 = c4× × × ×× 拓展延伸 (3)-a2·a 6 (4)a4(-a3)(-a)372532)2)(2(2)2)(1( 解(1)532)2(5322 532 82(2)722)2(7222 722 92 62 aa 62 a8a （ 3 ） （4）334))((aaa))((334aaa334aaa334a10a 4. 填空：（ 1 ） 8 = 2x ，则 x = ；（ 2 ） 8× 4 = 2x ，则 x = ；（ 3 ） 3×27×9 = 3x ，则 x = .35623 23 3253622 × = 33 32 × ×= 能力提高： 1. 如果 an-2 a‧n+1=a11,则 n= .6解：12  nnaa12nna12 na11a1112 n6n 解得 2. 已知：am=2 ， an=3. 求 am+n . nma解：nm aa 326 我学到了什么？ 知识 方法 同底数幂相乘， 底数 指数 am · an = am+n (m 、 n 正整数 ) “特殊→一般→特殊” 例子 公式 应用相加 .不变，