人教版高一数学y=Asinwxb的图象和性质 课件VIP免费

步入情境：xysin 前面你学习了正弦函数 的图象和性质 . 在物理和工程技术的许多问题中，经常会遇到形如 的函数，那么，它的图象如何作出？它的图象与 的图象又有什么关系？ )sin( xAyxysin)sin(xAy一、请思考： 你可以怎样作出函数 在一个周期的图象？)sin(323xy)sin(xAy1 、五点法作图2 、图象变换法 请回答下列问题： 1. 函数 的图象与 图象的关系？xysin)0(sinAxAy)sin(xAy2. 函数 的图象与 图象的关系？xysin)0(sinxy 3. 函数 的图象与 图象的关系？xysin)sin(xy 4. 函数 的图象与 图象的关系？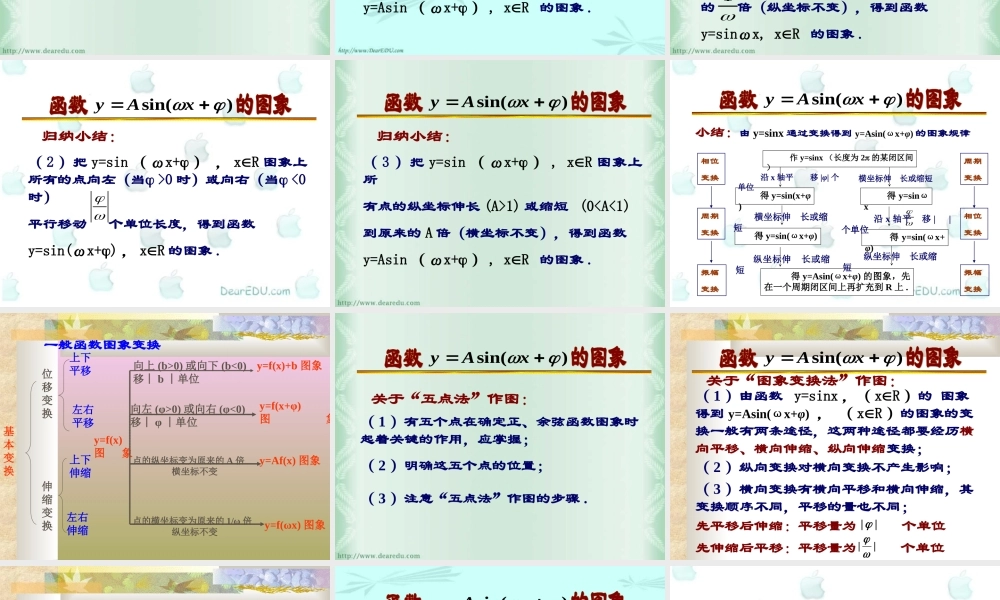xysin)0,0)(sin(AxAy归纳小结：一般地：函数 y=Asin(x+)(A>0 ， >0)的图象由 y=sinx 的图象经下列变换得到： （ 1 ）把 y=sinx ， xR 图象上所有的点向左（当 >0 时）或向右（当 <0 时）平行移动 || 个单位长度，得到函数 y=sin(x+) ， xR 的图象 .)sin(xAy归纳小结：（ 2 ）把 y=sin(x+) ， xR 图象上所有点的横坐标缩短 (ω>1) 或伸长 (0<ω<1) 到原来的 倍（纵坐标不变），得到函数y=sin （ ωx+ ） , xR 的图象 .1)sin(xAy归纳小结：（ 3 ）把 y=sin （ ωx+ ） , xR 图象上所有点的纵坐标伸长 (A>1) 或缩短 (00 ， >0)的图象也可由 y=sinx 的图象经下列变换得到： （ 1 ）把 y=sinx ， xR 图象上所有点的横坐标缩短 (ω>1) 或伸长 (0<ω<1) 到原来的 倍（纵坐标不变），得到函数y=sinωx, xR 的图象 .)sin(xAy1归纳小结：（ 2 ）把 y=sin （ ωx+ ） ， xR 图象上所有的点向左（当 >0 时）或向右（当 <0时）平行移动 个单位长度，得到函数y=sin(ωx+) ， xR 的图象 .)sin(xAy归纳小结：（ 3 ）把 y=sin （ ωx+ ） , xR 图象上所有点的纵坐标伸长 (A>1) 或缩短 (0