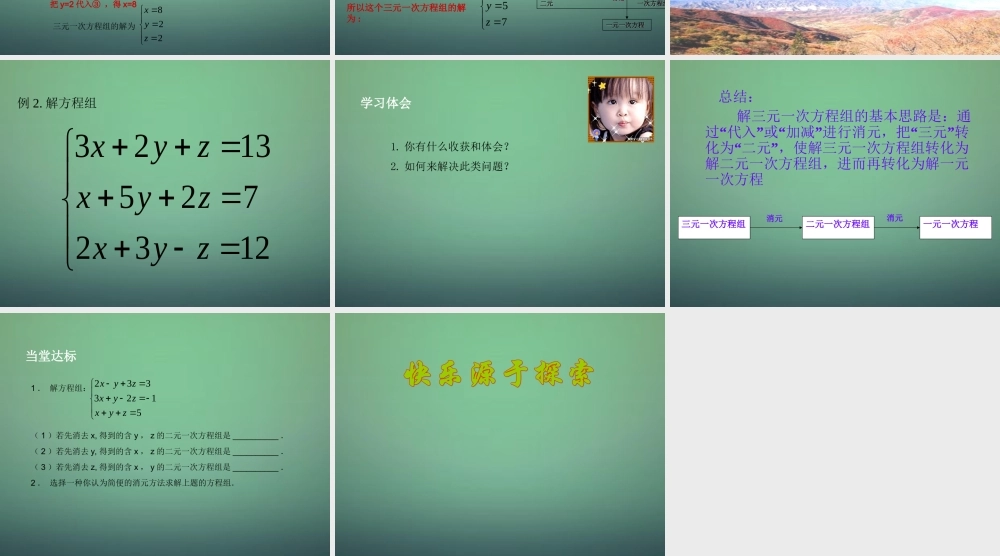
2 . 5 三元一次方程组及其解法情境引入1 、解二元一次方程组有哪几种方法?2 、它们的实质是什么? 二元一次方程组代入加减消元一元一次方程化未知为已知化归转化思想代入消元法和加减消元法消元法课中探究 小明手头有 12 张面额分别是 1 元、 2 元、 5 元的纸币,共计 22 元,其中 1 元纸币的数量是 2 元纸币数量的 4 倍.求 1元、 2 元、 5 元的纸币各多少张?想一想 这个问题中包含有 这个问题中包含有 个相 个相等关系:等关系:三三11 元纸币张数+元纸币张数+ 22 元纸币张数+元纸币张数+ 55 元纸币张数=元纸币张数= 1212张张11 元纸币的张数=元纸币的张数= 22 元纸币的张数的元纸币的张数的 44 倍倍11 元的金额+元的金额+ 22 元的金额+元的金额+ 55 元的金额=元的金额= 2222 元元课中探究做一做 根据以上分析,你能列出方程组吗?解:设设 11 元、元、 22 元、元、 55 元的纸币分别为元的纸币分别为 xx 张、张、 yy 张、张、 zz张张 . 观察这个方程组,是由 个 次方程组成的含有 _____ 个未知数的方程组 , 叫做___________________ . 说一说1225224xyzxyzxy 根据题意列方程组得三一三三元一次方程组讨论: 三元一次方程组怎么求解? 小明手头有 12 张面额分别是 1 元、 2 元、 5 元的纸币,共计 22 元,其中 1 元纸币的数量是 2 元纸币数量的 4 倍.求1 元、 2 元、 5 元的纸币各多少张?课中探究试一试:试着求解我们前面列出的三元一次方程组. 1225224xyzxyzxy ①②③把③分别代入①②,得5126522yzyz解这个二元一次方程组得2,2yz把 y=2 代入③ ,得 x=8822xyz 三元一次方程组的解为例 1. 解方程组2122xyzxyzxyz 所以这个三元一次方程组的解为 :57yz 257xyz ①②③课中探究解 : 将③ 分别代入① ②消去 x 得 : 解这个方程组得 :解三元一次方程组的基本思路是: 通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程。三元一次方程组三元一次方程组二元 一次方程组二元 一次方程组消元消元一元一次方程一元一次方程消元消元3212yzyz 将 ,...