yuankejian 课件VIP免费

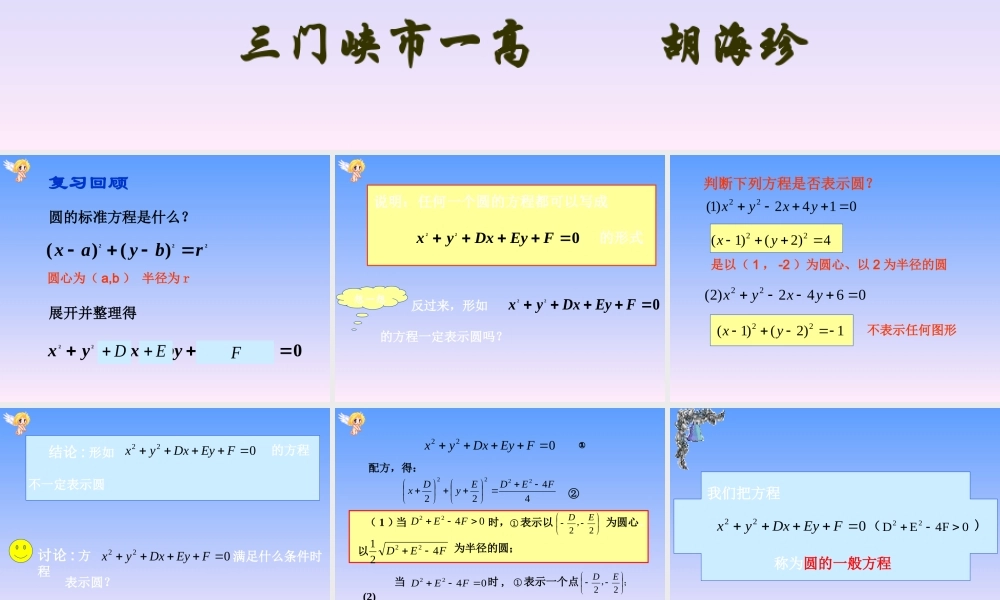
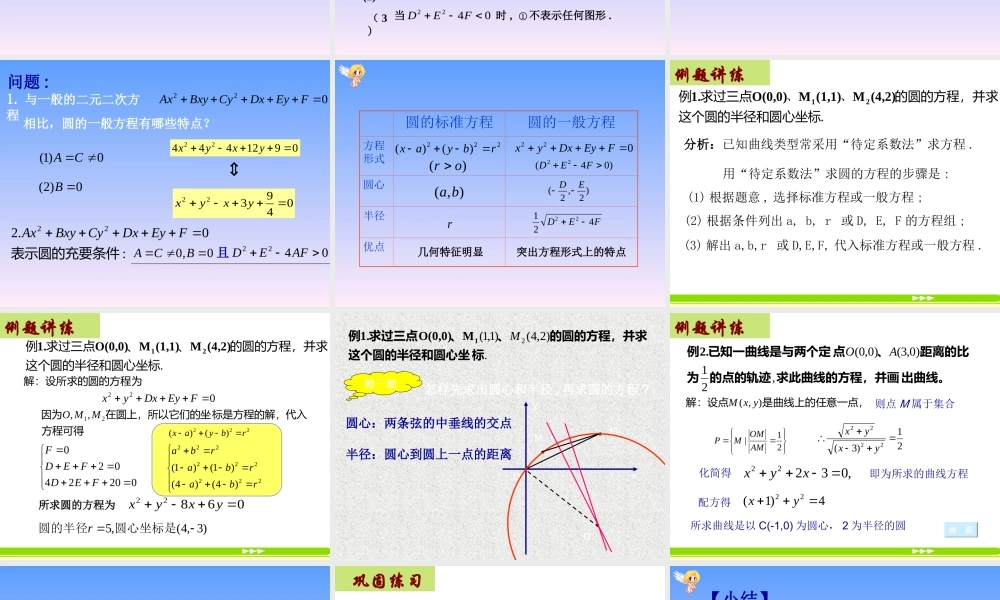
022FEyDxyx三门峡市一高 胡海珍复习回顾222)()(rbyax02222222rbabyaxyx展开并整理得圆的标准方程是什么？DEF圆心为（ a,b ） 半径为 r说明：任何一个圆的方程都可以写成022FEyDxyx的形式反过来，形如022FEyDxyx的方程一定表示圆吗？想一想 0142)1(22yxyx0642)2(22yxyx是以（ 1 ， -2 ）为圆心、以 2 为半径的圆 4)2()1(22yx1)2()1(22yx不表示任何图形判断下列方程是否表示圆？讨论 : 方程022FEyDxyx满足什么条件时表示圆？结论 : 形如022FEyDxyx的方程不一定表示圆配方，得：44222222FEDEyDx②① 表示一个点；，22ED0422FED (2)当时 ,① 不表示任何图形 .（ 3)0422FED当时 ,022FEyDxyx①（ 1 ）0422FED当时，22ED，① 表示以为圆心、FED42122以为半径的圆； (022FEyDxyx0F4ED22我们把方程称为圆的一般方程)（问题 ::0.222表示圆的充要条件FEyDxCyBxyAx00B,CA0)1(CA0)2(B091244422yxyx022FEyDxCyBxyAx1. 与一般的二元二次方程 相比，圆的一般方程有哪些特点？049322yxyx0422AFED且圆的标准方程圆的一般方程方程形式圆心半径优点222)()(rbyax)(or 022FEyDxyx)04(22FED),(ba)2,2(ED FED42122几何特征明显突出方程形式上的特点r 例题讲练.、、标这个圆的半径和圆心坐的圆的方程，并求求过三点例(4,2)M(1,1)MO(0,0)1.21分析：已知曲线类型常采用“待定系数法”求方程 .用“待定系数法”求圆的方程的步骤是 :(1) 根据题意 , 选择标准方程或一般方程 ;(2) 根据条件列出 a, b, r 或 D, E, F 的方程组 ;(3) 解出 a,b,r 或 D,E,F, 代入标准方程或一般方程 . 例题讲练.标这个圆的半径和圆心坐的圆的方程，并求、、求过三点例(4,2)M(1,1)MO(0,0)1.21为解：设所求的圆的方程方程可得标是方程的解，代入在圆上，所以它们的坐因为21,,MMO022FEyDxyx02024020FEDFEDF068FED所求圆的方程为06822yxyx)3,4(,5 圆心坐标是圆的半径r222)()(rbyax...