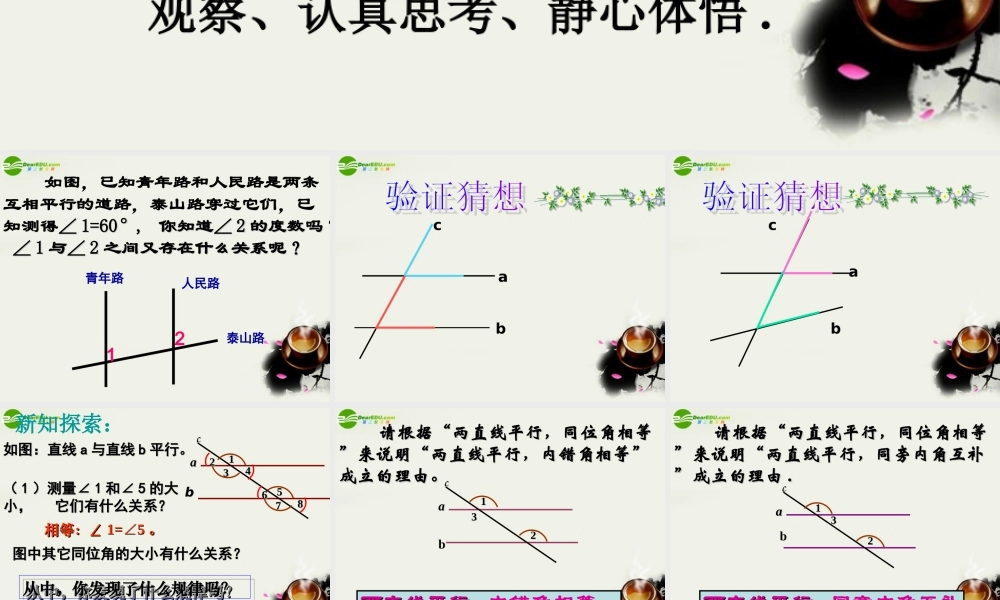
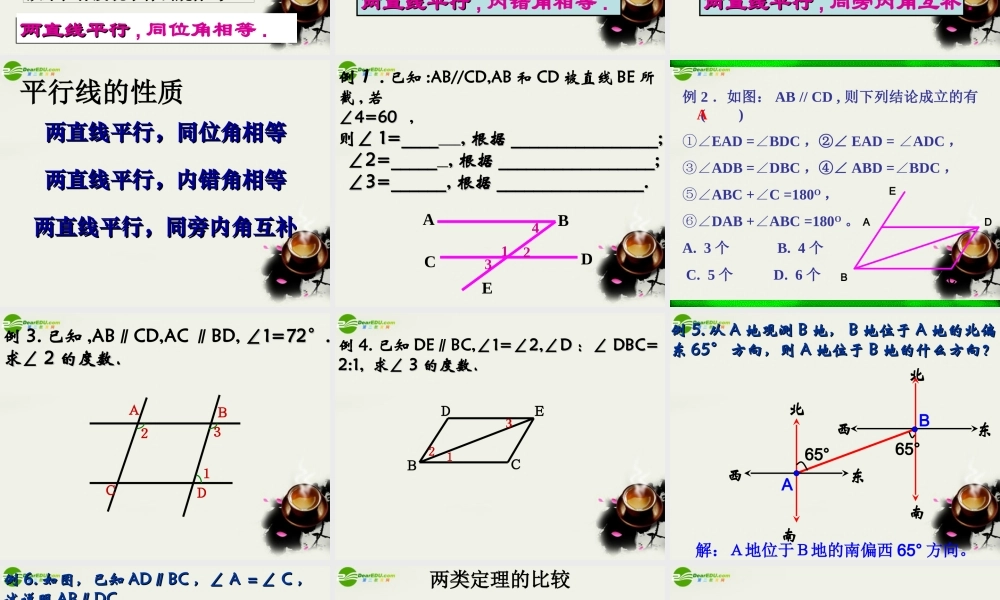
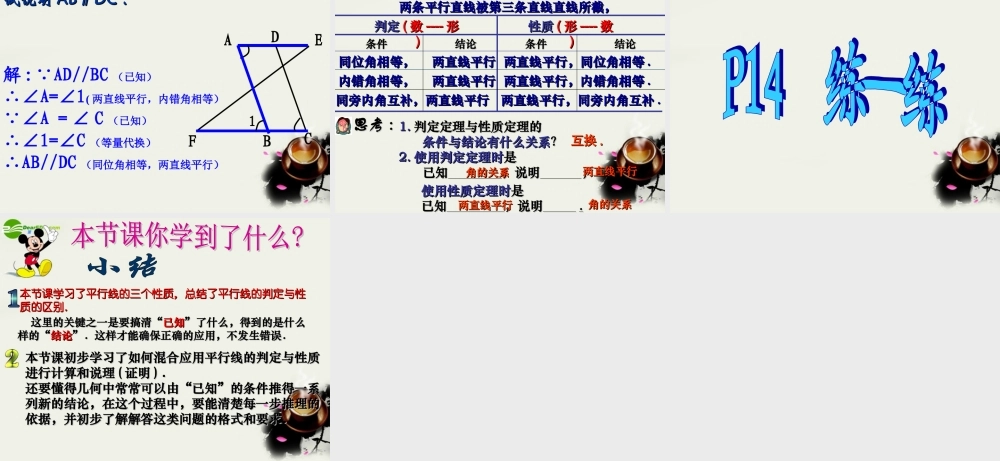
学会有条理的表达自己对数学问题的理解,就需要细心观察、认真思考、静心体悟 . 如图,已知青年路和人民路是两条互相平行的道路,泰山路穿过它们,已知测得∠∠ 1=60°, 1=60°, 你知道∠你知道∠ 22 的度数吗?的度数吗? ∠ ∠ 11 与∠与∠ 22 之间又存在什么关系呢?之间又存在什么关系呢?青年路人民路泰山路12 abc abc新知探索:bb如图:直线如图:直线 aa 与直线与直线 bb 平行。平行。(( 11 ))测量∠测量∠ 11 和∠和∠ 55 的大的大小, 它们有什么关系?小, 它们有什么关系?相等:∠相等:∠ 1=5∠1=5∠ 。。图中其它同位角的大小有什么关系?图中其它同位角的大小有什么关系?从中,你发现了什么规律吗?从中,你发现了什么规律吗?从中,你发现了什么规律吗?从中,你发现了什么规律吗?5533aacc881122447766两直线平行两直线平行 , 同位角相等 . 请根据“两直线平行,同位角相等请根据“两直线平行,同位角相等”来说明“两直线平行,内错角相等””来说明“两直线平行,内错角相等”成立的理由。成立的理由。33aacc1122b两直线平行两直线平行 , 内错角相等 .aacc113322b两直线平行两直线平行 , 同旁内角互补 . 请根据“两直线平行,同位角相等请根据“两直线平行,同位角相等”来说明“两直线平行,同旁内角互补”来说明“两直线平行,同旁内角互补”成立的理由”成立的理由 .. 平行线的性质两直线平行,同位角相等两直线平行,同位角相等两直线平行,内错角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,同旁内角互补例1 . 已知 :AB//CD,AB 和 CD 被直线 BE 所截 , 若∠∠4=604=60 º,则∠∠ 1=____1=____________,, 根据根据 ________________;________________; ∠ ∠2=_____2=_________,, 根据根据 _________________;_________________; ∠ ∠3=______,3=______, 根据根据 ________________.________________.ABCDE4123 例 2 .如图: AB // CD , 则下列结论成立的有 ( )①∠EAD =BDC∠,②∠ EAD = ADC∠,③∠ADB =DBC∠,④∠ ABD =BDC∠,⑤∠ABC +C =180∠O ,⑥∠DAB +ABC =180∠O 。A. 3 个 B. 4 个 C. 5 个 D. 6 个 EDCABA例 3. 已知 ,AB∥CD,AC ∥BD, ∠1=72∠1=72°.°.求求∠∠ 22 的度数.的度数.ABCD231例 4. 已知 DE∥BC,∠1=∠2,∠D∠1=∠2,∠D :∠:∠ DBC=...