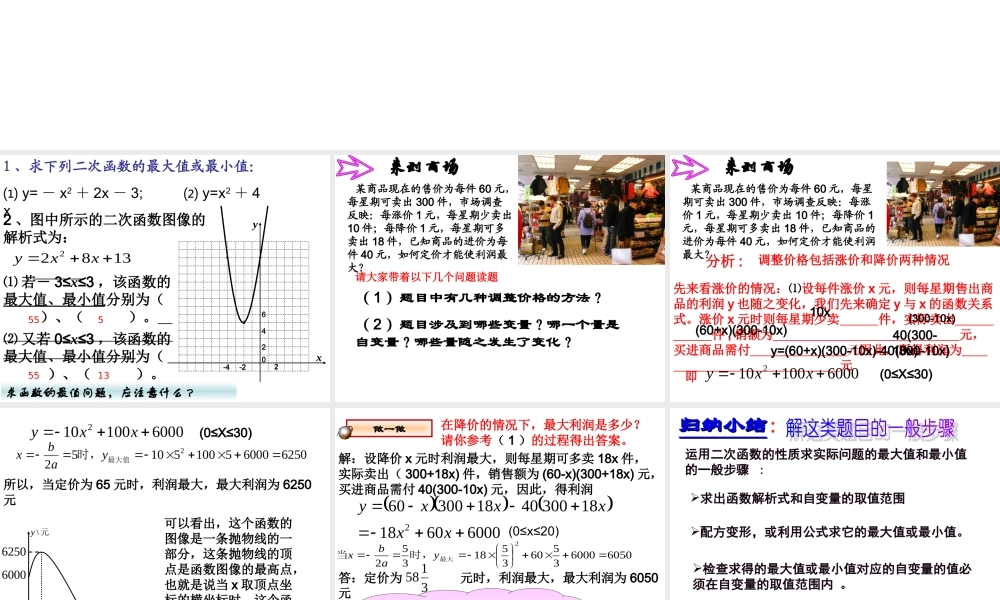
-202462-4xy⑴ 若- 3≤x≤3 ,该函数的最大值、最小值分别为( )、( )。 ⑵ 又若 0≤x≤3 ,该函数的最大值、最小值分别为( )、( )。求函数的最值问题,应注意什么 ?55 555 132 、图中所示的二次函数图像的解析式为: 13822xxy1 、求下列二次函数的最大值或最小值: ⑴ y= - x2 + 2x - 3; y=x⑵2 + 4x 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:每涨价 1 元,每星期少卖出10 件;每降价 1 元,每星期可多卖出 18 件,已知商品的进价为每件 40 元,如何定价才能使利润最大?请大家带着以下几个问题读题( 1 )题目中有几种调整价格的方法? ( 2 )题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化? 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:每涨价 1 元,每星期少卖出 10 件;每降价 1元,每星期可多卖出 18 件,已知商品的进价为每件 40 元,如何定价才能使利润最大?分析 :调整价格包括涨价和降价两种情况先来看涨价的情况:⑴设每件涨价 x 元,则每星期售出商品的利润 y 也随之变化,我们先来确定 y 与 x 的函数关系式。涨价 x 元时则每星期少卖 件,实际卖出 件 , 销额为 元,买进商品需付 元因此,所得利润为 元10x(300-10x)(60+x)(300-10x)40(300-10x)y=(60+x)(300-10x)-40(300-10x)即6000100102xxy(0≤X≤30) 6000100102xxy(0≤X≤30)625060005100510522最大值时,yabx可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当 x 取顶点坐标的横坐标时,这个函数有最大值。由公式可以求出顶点的横坐标 .元\x元\y625060005300所以,当定价为 65 元时,利润最大,最大利润为 6250元 在降价的情况下,最大利润是多少?请你参考( 1 )的过程得出答案。解:设降价 x 元时利润最大,则每星期可多卖 18x 件,实际卖出( 300+18x) 件,销售额为 (60-x)(300+18x) 元,买进商品需付 40(300-10x) 元,因此,得利润60506000356035183522最大时,当yabx答:定价为 元时,利润最大,最大利润为 6050元 3158做一做由 (1)(2) 的讨论及现在的销售情况 , 你知道应该如何定价能使利润最大了吗 ?60006018183004018300602...