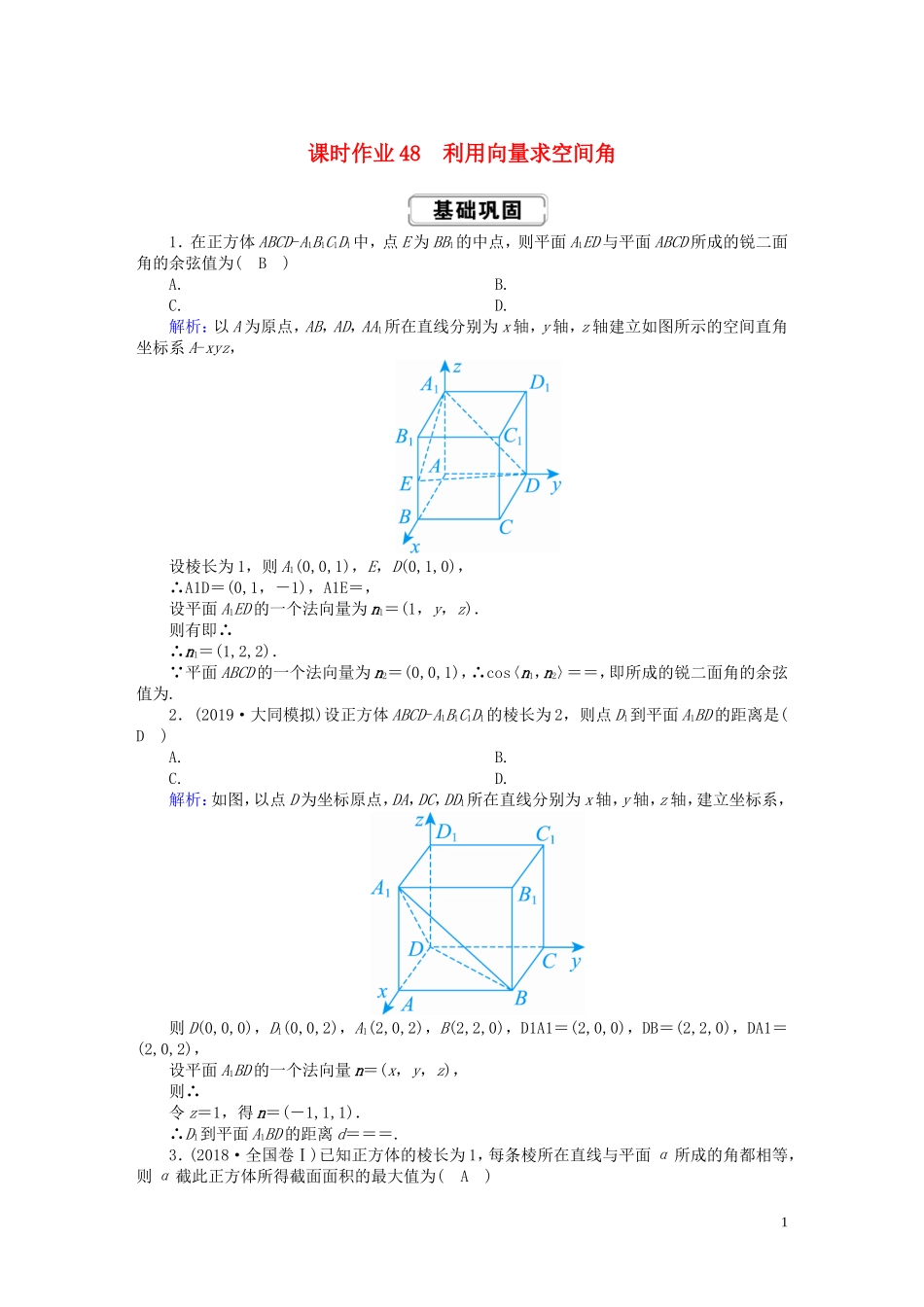
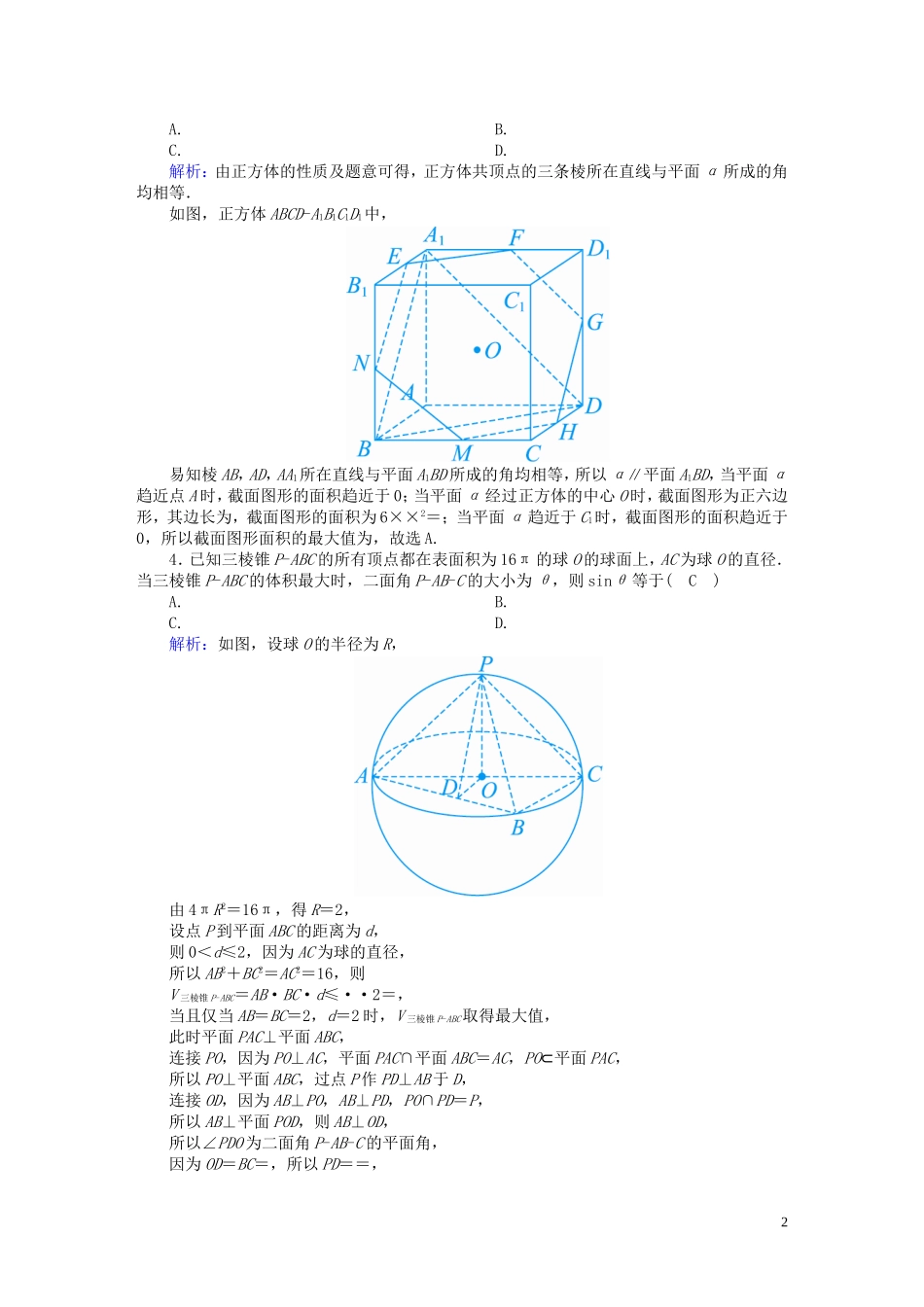
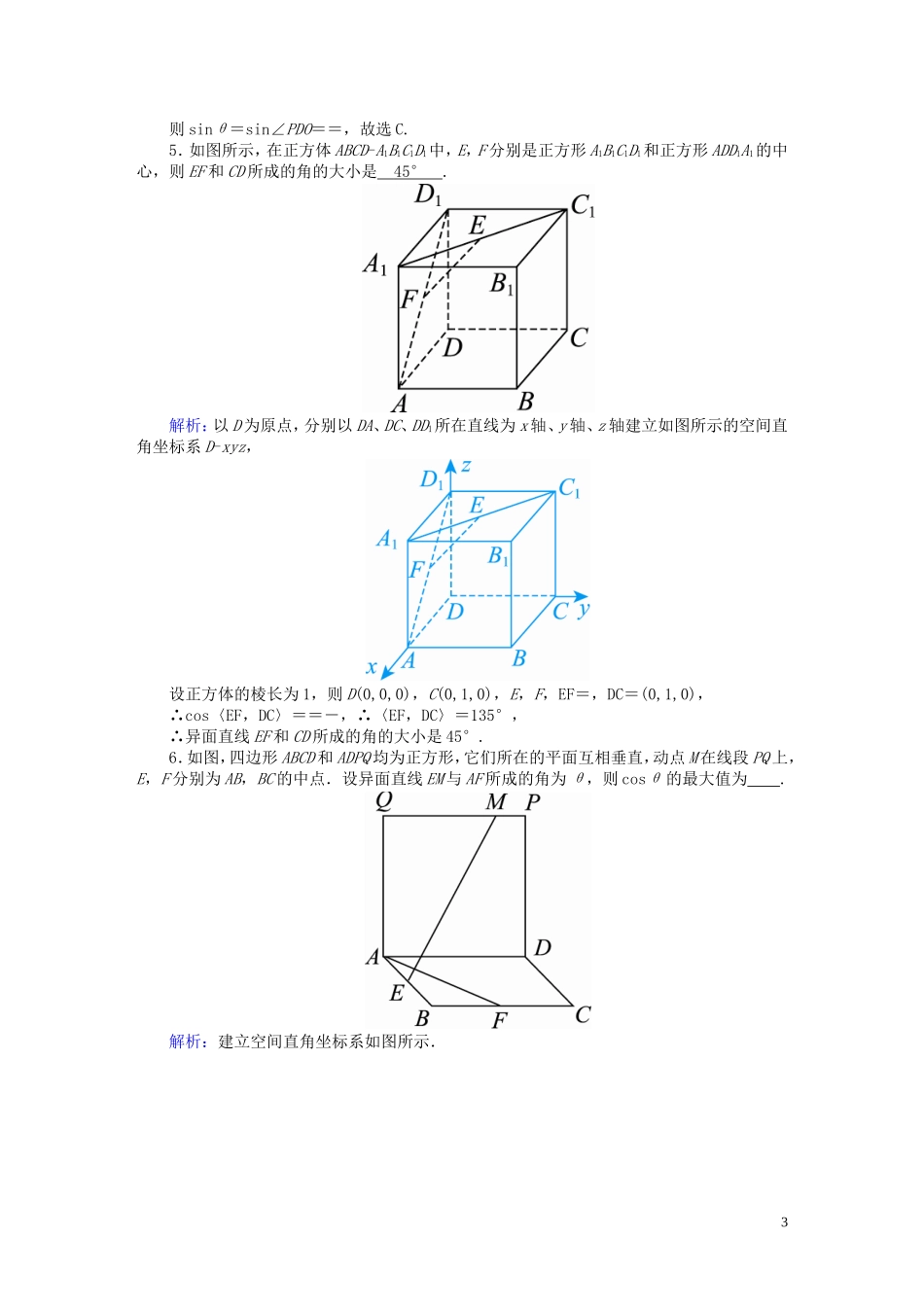
课时作业 48 利用向量求空间角1.在正方体 ABCD-A1B1C1D1中,点 E 为 BB1的中点,则平面 A1ED 与平面 ABCD 所成的锐二面角的余弦值为( B )A. B.C. D.解析:以 A 为原点,AB,AD,AA1所在直线分别为 x 轴,y 轴,z 轴建立如图所示的空间直角坐标系 A-xyz,设棱长为 1,则 A1(0,0,1),E,D(0,1,0),∴A1D=(0,1,-1),A1E=,设平面 A1ED 的一个法向量为 n1=(1,y,z).则有即∴∴n1=(1,2,2). 平面 ABCD 的一个法向量为 n2=(0,0,1),∴cos〈n1,n2〉==,即所成的锐二面角的余弦值为.2.(2019·大同模拟)设正方体 ABCD-A1B1C1D1的棱长为 2,则点 D1到平面 A1BD 的距离是( D )A. B.C. D.解析:如图,以点 D 为坐标原点,DA,DC,DD1所在直线分别为 x 轴,y 轴,z 轴,建立坐标系,则 D(0,0,0),D1(0,0,2),A1(2,0,2),B(2,2,0),D1A1=(2,0,0),DB=(2,2,0),DA1=(2,0,2),设平面 A1BD 的一个法向量 n=(x,y,z),则∴令 z=1,得 n=(-1,1,1).∴D1到平面 A1BD 的距离 d===.3.(2018·全国卷Ⅰ)已知正方体的棱长为 1,每条棱所在直线与平面 α 所成的角都相等,则 α 截此正方体所得截面面积的最大值为( A )1A. B.C. D.解析:由正方体的性质及题意可得,正方体共顶点的三条棱所在直线与平面 α 所成的角均相等.如图,正方体 ABCD-A1B1C1D1中,易知棱 AB,AD,AA1所在直线与平面 A1BD 所成的角均相等,所以 α∥平面 A1BD,当平面 α趋近点 A 时,截面图形的面积趋近于 0;当平面 α 经过正方体的中心 O 时,截面图形为正六边形,其边长为,截面图形的面积为 6××2=;当平面 α 趋近于 C1时,截面图形的面积趋近于0,所以截面图形面积的最大值为,故选 A.4.已知三棱锥 P-ABC 的所有顶点都在表面积为 16π 的球 O 的球面上,AC 为球 O 的直径.当三棱锥 P-ABC 的体积最大时,二面角 P-AB-C 的大小为 θ,则 sinθ 等于( C )A. B.C. D.解析:如图,设球 O 的半径为 R,由 4πR2=16π,得 R=2,设点 P 到平面 ABC 的距离为 d,则 0<d≤2,因为 AC 为球的直径,所以 AB2+BC2=AC2=16,则V 三棱锥 P-ABC=AB·BC·d≤··2=,当且仅当 AB=BC=2,d=2 时,V 三棱锥 P-ABC取得最大值,此时平面 PAC⊥平面 ABC,连接 PO,因为 PO⊥AC,平面 PAC∩平面 ABC=AC,PO⊂平面 PAC,所以 PO⊥平面 ...