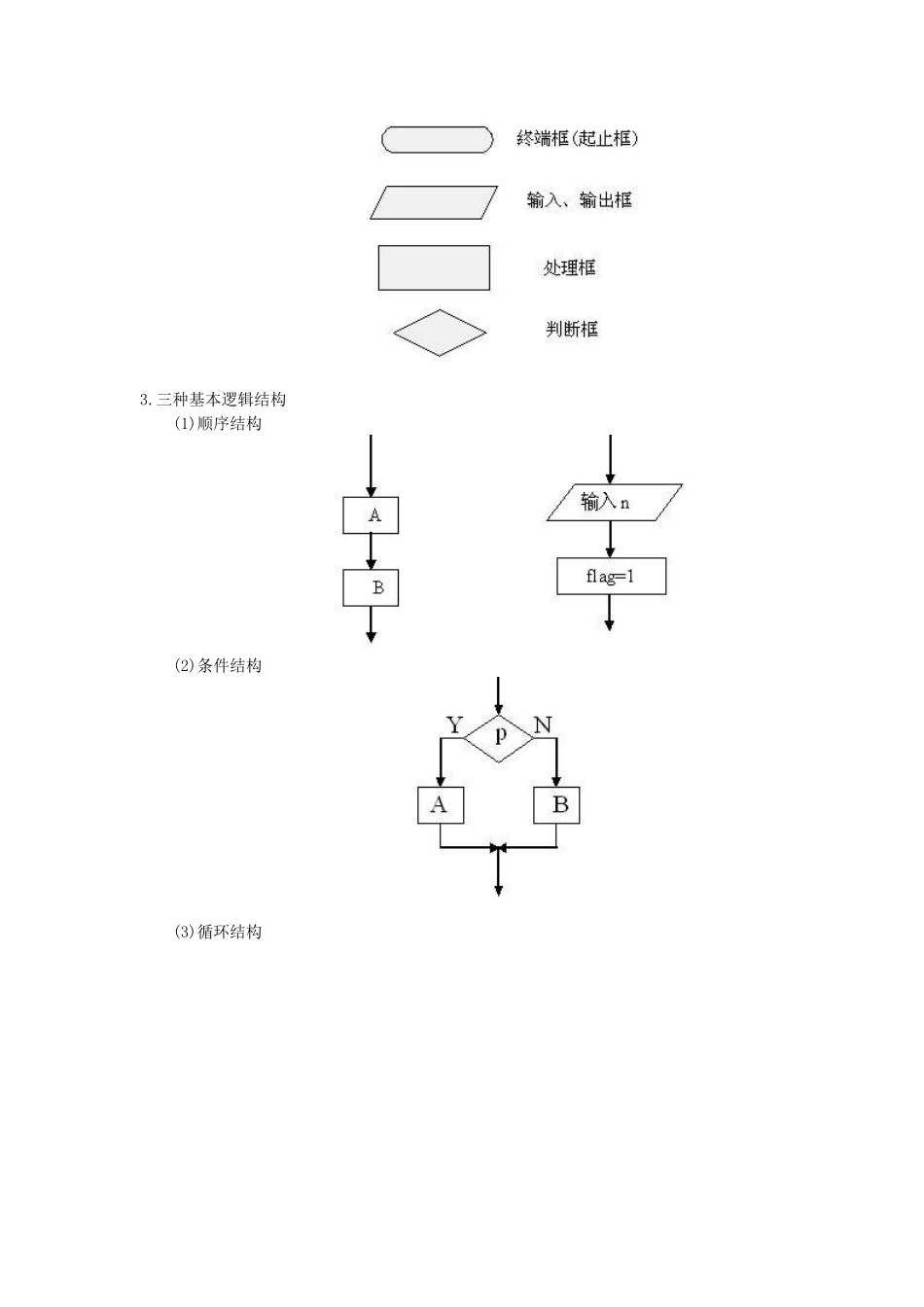
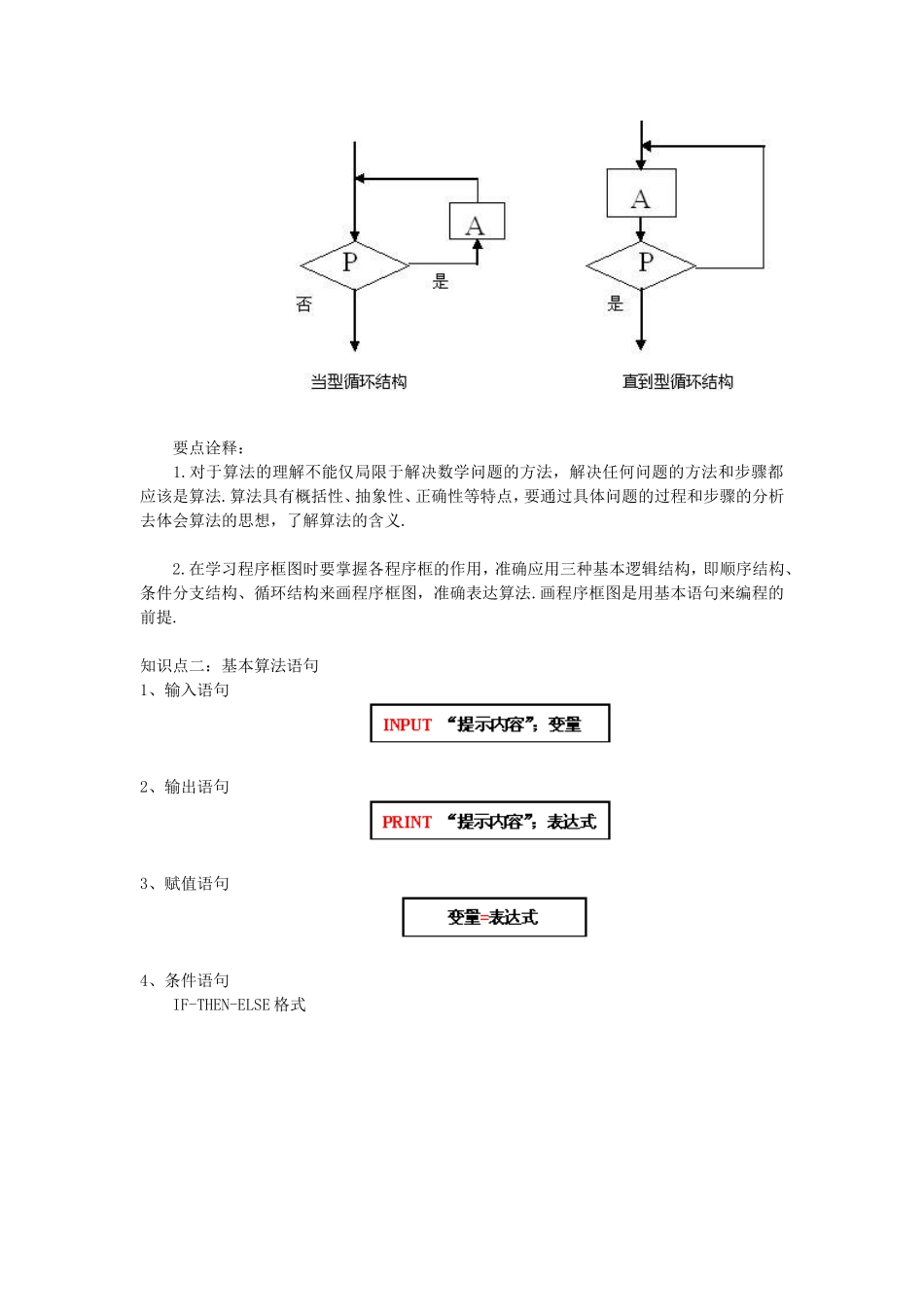
高二数学算法与程序框图复习与巩固一、知识网络 二、目标认知学习目标: 1.明确算法的含义,熟悉算法的三种基本结构:顺序、条件和循环,以及基本的算法语句. 2.能熟练运用辗转相除法与更相减损术、秦九韶算法、进位制等典型的算法知识解决同类问题.重点: 算法的基本知识与算法对应的程序框图的设计.难点: 与算法对应的程序框图的设计及算法程序的编写.三、知识要点梳理知识点一:算法与程序框图1.算法的定义: 广义的算法是指完成某项工作的方法和步骤,现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.2.四种基本的程序框 3.三种基本逻辑结构 (1)顺序结构 (2)条件结构 (3)循环结构 要点诠释: 1.对于算法的理解不能仅局限于解决数学问题的方法,解决任何问题的方法和步骤都应该是算法.算法具有概括性、抽象性、正确性等特点,要通过具体问题的过程和步骤的分析去体会算法的思想,了解算法的含义. 2.在学习程序框图时要掌握各程序框的作用,准确应用三种基本逻辑结构,即顺序结构、条件分支结构、循环结构来画程序框图,准确表达算法.画程序框图是用基本语句来编程的前提.知识点二:基本算法语句1、输入语句 2、输出语句 3、赋值语句 4、条件语句 IF-THEN-ELSE 格式 IF-THEN 格式 5、循环语句 (1)WHILE 语句 (2)UNTIL 语句 要点诠释: 基本算法语句是程序设计语言的组成部分,注意各语句的作用,准确理解赋值语句,灵活表达条件语句.计算机能够直接或间接理解的程序语言都包含输入语句、输出语句、赋值语句、条件语句和循环语句等基本算法语句.输入语句、输出语句和赋值语句贯穿于大多数算法的结构中,而算法中的条件结构由条件语句来表述,循环结构由循环语句来实现.学习中要熟练掌握这些基本算法语句.知识点三:算法案例案例 1、辗转相除法与更相减损术 1.利用辗转相除法求最大公约数的步骤如下: (1)用较大的数 m 除以较小的数 n 得到一个商和一个余数; (2)若=0,则 n 为 m,n 的最大公约数;若≠0,则用除数 n 除以余数得到一个商和一个余数; (3)若=0,则为 m,n 的最大公约数;若≠0,则用除数除以余数得到一个商和一个余数;…… 依次计算直至=0,此时所得到的即为所求的最大公约数. 2.更相减损术 (1)任意给出两个正数;判断它们是否都是偶数.若是,用 2 约简;若不是,执行第二步. (2)以较大的数减去...