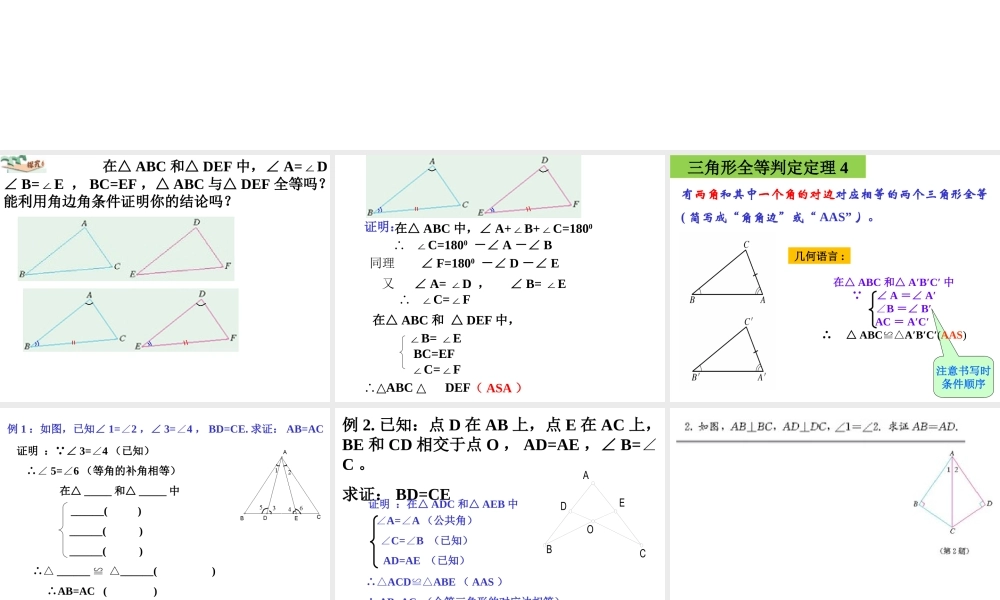
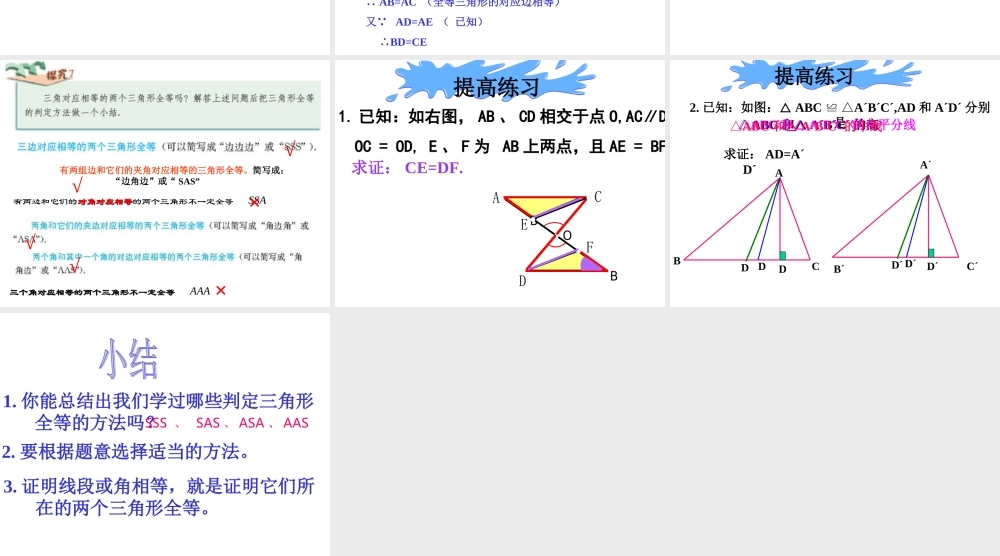
AAS 在△ ABC 和△ DEF 中,∠ A=D∠,∠ B=E ∠, BC=EF ,△ ABC 与△ DEF 全等吗?能利用角边角条件证明你的结论吗?在△ ABC 中,∠ A+B+C=180∠∠0证明: ∴ ∠C=1800 -∠ A -∠ B同理 ∠ F=1800 -∠ D -∠ E又 ∠ A= D ∠, ∠ B= E∠在△ ABC 和 △ DEF 中, ∴ ∠C=F∠∠B= E∠∠C=F∠BC=EF∴△ABC △ DEF△( ASA )注意书写时条件顺序三角形全等判定定理 4有两角和其中一个角的对边对应相等的两个三角形全等( 简写成“角角边”或“ AAS” )。几何语言 : 在△ ABC 和△ A′B′C′ 中∵ ∠ A =∠ A′ ∠B =∠ B′ AC = A′C′∴ △ ABCA′B′C′≌△(AAS)例 1 :如图,已知∠ 1=2∠ ,∠ 3=4∠ , BD=CE. 求证: AB=AC证明 :∵∠ 3=4∠ (已知) ∴∠ 5=6∠ (等角的补角相等) 在△ _____ 和△ _____ 中 ______( ) ______( ) ______( ) ∴△ ______ ______( )≌ △ ∴AB=AC ( )例 2. 已知:点 D 在 AB 上,点 E 在 AC 上,BE 和 CD 相交于点 O , AD=AE ,∠ B=∠C 。求证: BD=CE 证明 :在△ ADC 和△ AEB 中∠A=A∠(公共角)∠C=B ∠(已知)AD=AE (已知)∴△ACDABE≌△( AAS ) ∴ AB=AC (全等三角形的对应边相等)又∵ AD=AE ( 已知) ∴BD=CEDBEAOC有两组边和它们的夹角对应相等的三角形全等。简写成:“边角边”或“ SAS”有两边和它们的对角对应相等对角对应相等的两个三角形不一定全等SSA×三个角对应相等角对应相等的两个三角形不一定全等AAA×√√√√OBCDBAFE提高练习1. 已知:如右图, AB 、 CD 相交于点 O,AC∥DB, OC = OD, E 、 F 为 AB 上两点,且 AE = BF.求证: CE=DF.BACA´B´C´△ABC 和△ A´B´C´ 的高DD´2. 已知:如图:△ ABC ≌ A△ ´B´C´,AD 和 A´D´ 分别 是 求证: AD=A´D´△ABC 和△ A´B´C´ 的角平分线DD´△ABC 和△ A´B´C´ 的中线 DD´提高练习1. 你能总结出我们学过哪些判定三角形 全等的方法吗?2. 要根据题意选择适当的方法。3. 证明线段或角相等,就是证明它们所 在的两个三角形全等。SSS 、 SAS 、 ASA 、 AAS