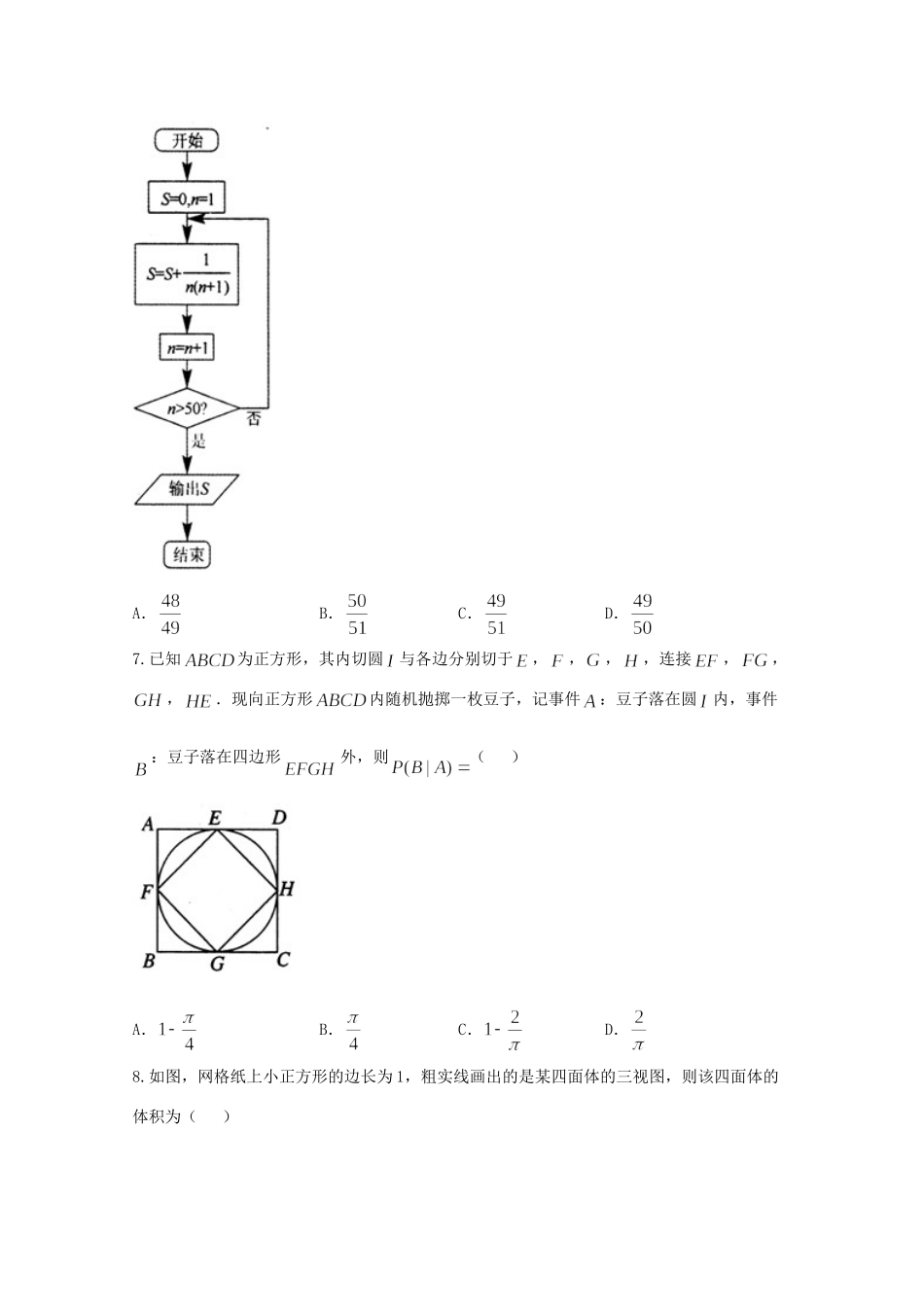
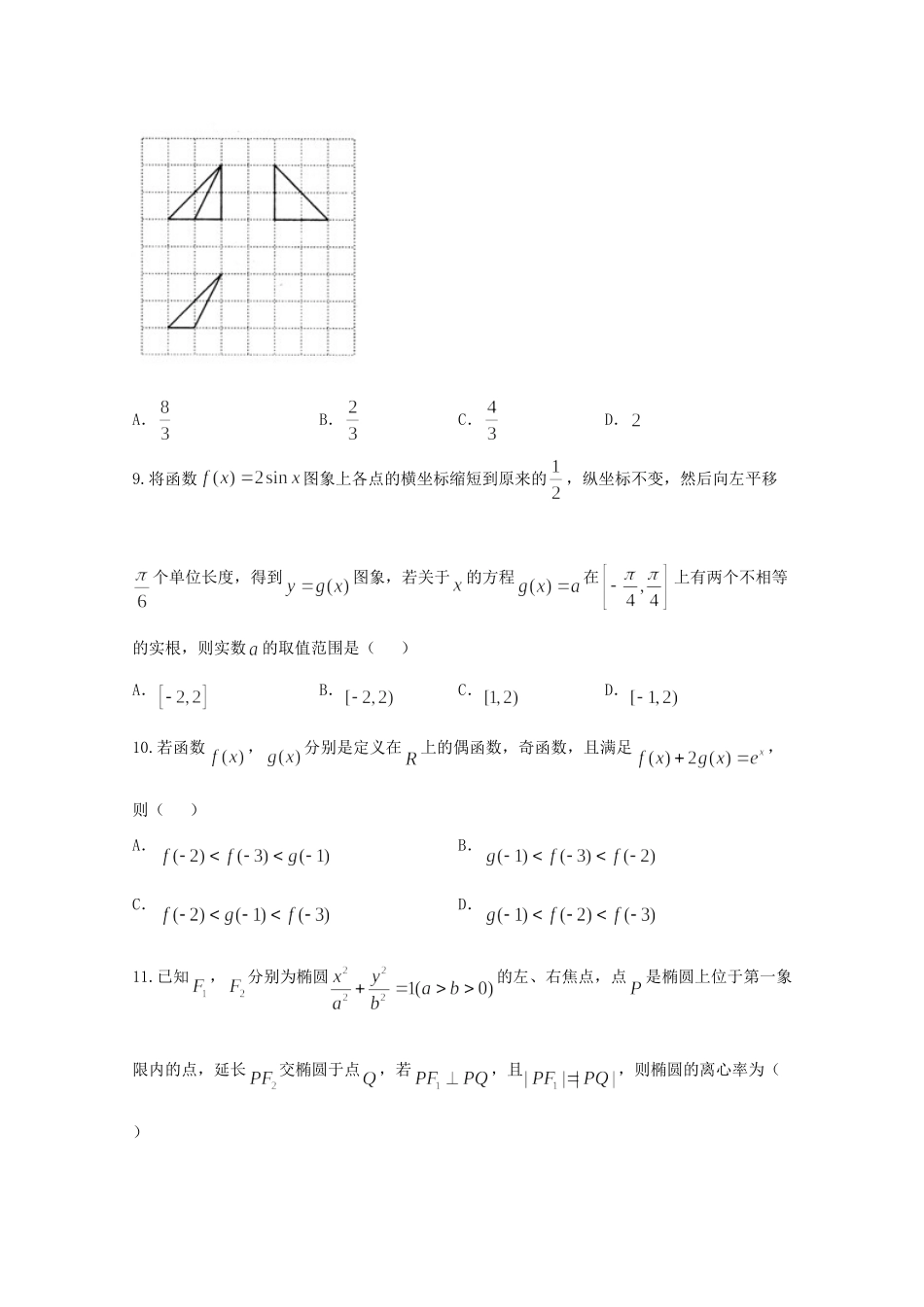
济南外国语学校高考模拟考试(二)理科数学第Ⅰ卷(共 60 分)一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则( )A.B.C.D. 2.若复数满足,其中 为虚数单位,则( )A.B.C.D. 3.已知命题:,:,则是的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.函数的部分图像可能是( )5.已知双曲线(,)与椭圆有共同焦点,且双曲线的一条渐近线方程为,则该双曲线的方程为( )A.B.C.D. 6.执行如图所示的程序框图,则输出的值为( )A.B.C.D. 7.已知为正方形,其内切圆与各边分别切于,,,,连接,,,.现向正方形内随机抛掷一枚豆子,记事件:豆子落在圆内,事件:豆子落在四边形外,则( )A.B.C.D. 8.如图,网格纸上小正方形的边长为 1,粗实线画出的是某四面体的三视图,则该四面体的体积为( )A.B.C.D. 9.将函数图象上各点的横坐标缩短到原来的,纵坐标不变,然后向左平移个单位长度,得到图象,若关于的方程在上有两个不相等的实根,则实数的取值范围是( )A.B.C.D. 10.若函数,分别是定义在上的偶函数,奇函数,且满足,则( )A.B.C.D. 11.已知,分别为椭圆的左、右焦点,点是椭圆上位于第一象限内的点,延长交椭圆于点,若,且,则椭圆的离心率为( )A.B.C.D. 12.为推导球的体积公式,刘徽制造了一个牟合方盖(在一个正方体内作两个互相垂直的内切圆柱,这两个圆柱的公共部分叫做牟合方盖),但没有得到牟合方盖的体积.200 年后,祖暅给出牟合方盖的体积计算方法,其核心过程被后人称为祖暅原理:缘幂势既同,则积不容异.意思是,夹在两个平行平面间的两个几何体被平行于这两个平行平面的任意平面所截,如果截面的面积总相等,那么这两个几何体的体积也相等.现在截取牟合方盖的八分之一,它的外切正方体的棱长为 1,如图所示,根据以上信息,则该牟合方盖的体积为( )A.B.C.D. 第Ⅱ卷(共 90 分)二、填空题(每题 5 分,满分 20 分,将答案填在答题纸上)13.已知的展开式各项系数之和为 256,则展开式中含项的系数为 .14.设等差数列的前项和为,若,,则公差 .15.在中,,其面积为 3,设点在内,且满足,则 .16.对,,使得不等式成立,则实数的取值范围是 .三、解答题 (本大题共 6 小题,共 70 分.解答应写出文字说...