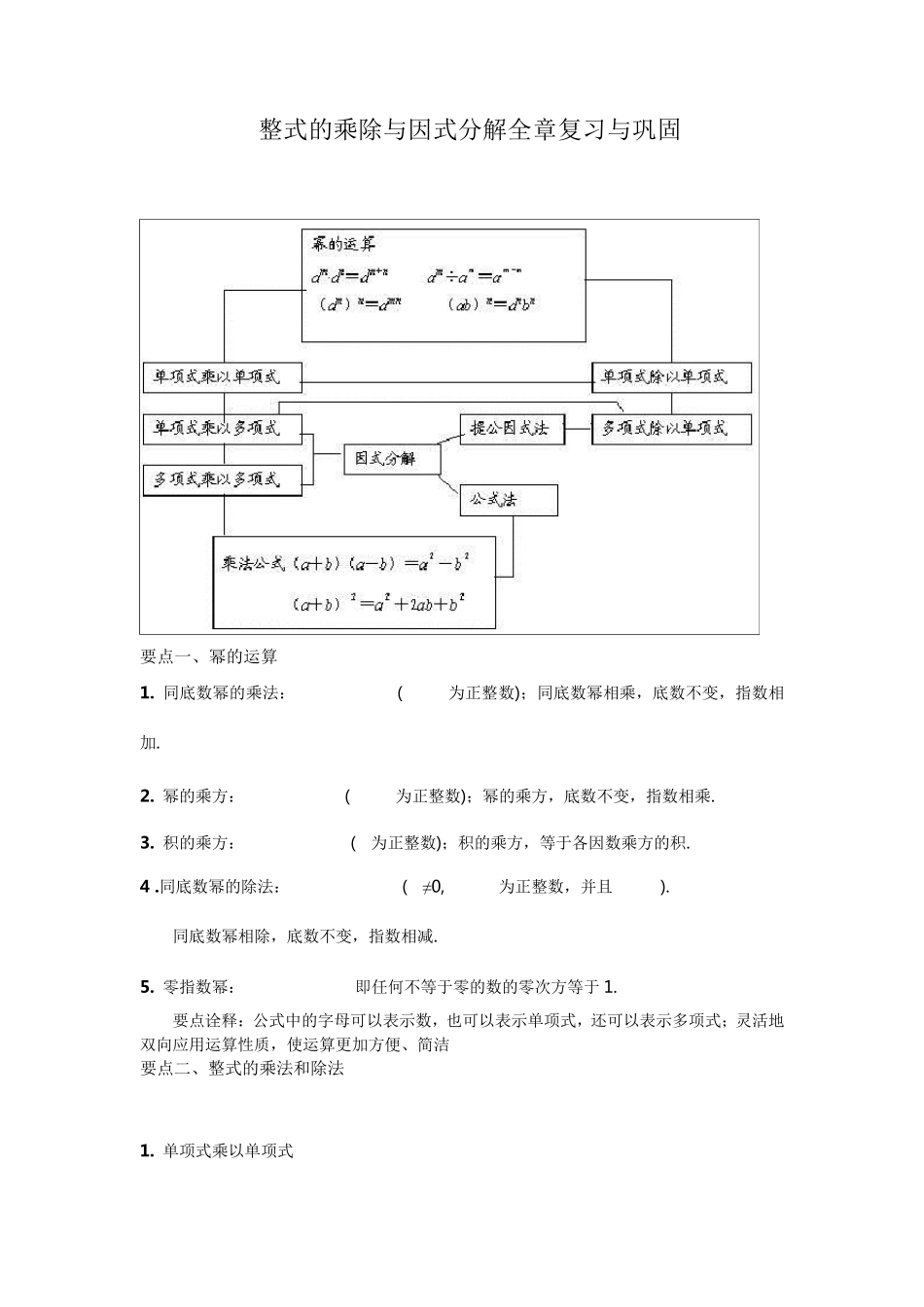
整式的乘除与因式分解全章复习与巩固 要点一、幂的运算 1. 同底数幂的乘法:(为正整数);同底数幂相乘,底数不变,指数相加. 2. 幂的乘方: (为正整数);幂的乘方,底数不变,指数相乘. 3. 积的乘方: (为正整数);积的乘方,等于各因数乘方的积. 4 .同底数幂的除法:(≠0, 为正整数,并且). 同底数幂相除,底数不变,指数相减. 5. 零指数幂:即任何不等于零的数的零次方等于 1. 要点诠释:公式中的字母可以表示数,也可以表示单项式,还可以表示多项式;灵活地双向应用运算性质,使运算更加方便、简洁 要点二、整式的乘法和除法 1. 单项式乘以单项式 单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. 2. 单项式乘以多项式 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加. 即(都是单项式). 3. 多项式乘以多项式 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加. 即. 要点诠释:运算时,要注意积的符号,多项式中的每一项前面的“+”“-”号是性质符号,单项式乘以多项式各项的结果,要用“+”连结,最后写成省略加号的代数和的形式.根据多项式的乘法,能得出一个应用比较广泛的公式:. 4. 单项式相除 把系数、相同字母的幂分别相除作为商的因式,对于只在被除式里出现的字母,则连同它的指数一起作为商的一个因式 要点三、乘法公式 1. 平方差公式: 两个数的和与这两个数的差的积,等于这两个数的平方差. 要点诠释:在这里,既可以是具体数字,也可以是单项式或多项式. 平方差公式的典型特征:既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方. 2 . 完全平方公式:; 两数和 (差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍. 要点诠释:公式特点:左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍 要点四、因式分解 把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式. 因式分解的方法主要有: 提公因式法, 公式法, 分组分解法, 十字相乘法, 添、拆项法等. 要点诠释: 落实好方法的综合运用: 首先提取公因式,然后考虑用公式; 两项平方或立方,三项完全或十字; 四项以上想分组,分组分得要合适...