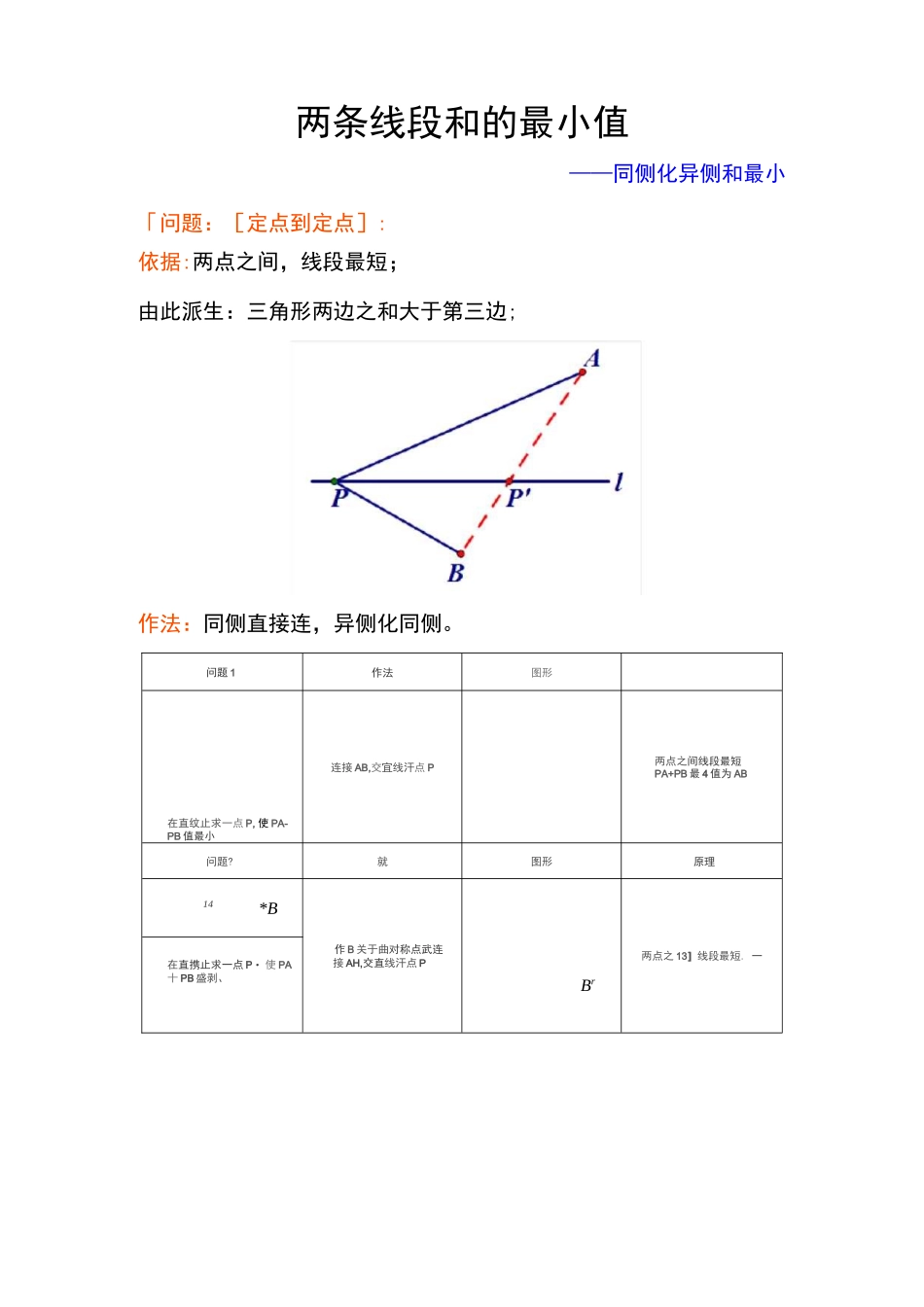
两条线段和的最小值——同侧化异侧和最小「问题:[定点到定点]:依据:两点之间,线段最短;由此派生:三角形两边之和大于第三边;作法:同侧直接连,异侧化同侧。问题 1作法图形在直纹止求一点 P, 使 PA-PB 值最小连接 AB,交宜线汗点 P两点之间线段最短PA+PB 最 4 值为 AB问题?就图形原理14*B作 B 关于曲对称点武连 接 AH,交直线汗点 P两点之 13]线段最短. 一在直携止求一点 P ・ 使 PA十 PB 盛剥、Br例题讲解:1.在锐角三角形 ABC 中,BC=4,ZABC=60°, BD 平分 ZABC,交 AC 于点 D,M,N 分别是BD,BC 上的动点,则 CM + MN 的最小值是.【分析】从已知条件结合图形认真思考,通过构造全等三角形, 转化线段,利用三角形的三边的关系确定线段和的最小值.【解答】解:如图,在 BA 上截取 BE = BN,因为乙 ABC 的平分线 交 AC 于点 D,所以 ZEBM = ZNBM,易证 ABME 三△BMN (SAS),所以 ME=MN .所以 CM + MN = CM + ME^CE .因为 CM + MN 有最小值.当C, M, E,三点共线,且 CE1 扉时,CE 是点 C 到直线 AB 的距离时,即 C 到直线 AB 的垂线段时,CE 取最小值为:4xsin60=2V3变式练习:如图,在锐角 AABC 中,AB=4,ZBAC=45°,ZBAC 的平分线交 BC 于点 D, M、N 分别是 AD 和 AB 上的动点,则 BM + MN 的最小值是.简析:本题的问题也在于动线段 BM、MN 居于动点轨迹AD 的同侧,同样把点 N 沿 AD 翻折至 AC 上,BM + MN = BM + MN',转化为求点 B 到直线 AC 的最短路径,即 BN'IAC 时,最小值为 2/22.如图,在矩形 ABCD 中,AB = 10,BC = 5 .若点M、N 分别是线段 AC,AB 上的两个动点,则 BM + MN 的最小 值为.达标检测1 如图,已知等边^ABC 的边长为 6,点 D 为 AC 的中点,点 E为 BC 的中点,点 P 为 BD 上一点,则 PE+PC 的最小值为.2. 如图,正方形 ABCD 的边长为 3, E 在 BC 上,且 BE=2, P 在 BD 上,贝 I] PE+PC 的最小值 为.3. 如图,矩形 ABCD 中,AD=5, AB=12,点 M 在 AC 上,点 N 在 AB 上,则 BM+MN 的最4.如图,菱形 ABCD 中,AB=2, ZBAD=60°, E、F、P 分别是 AB、BC、AC 上的动点, PE+PF 的最小值等于.5.在直角坐标系中,已知点 A (-3, 2), B (2, -4),在 x 轴上找一点 C,使 AC+BC 最 短,则点C 的坐标为.6.直角梯形 ABCD 中,A...