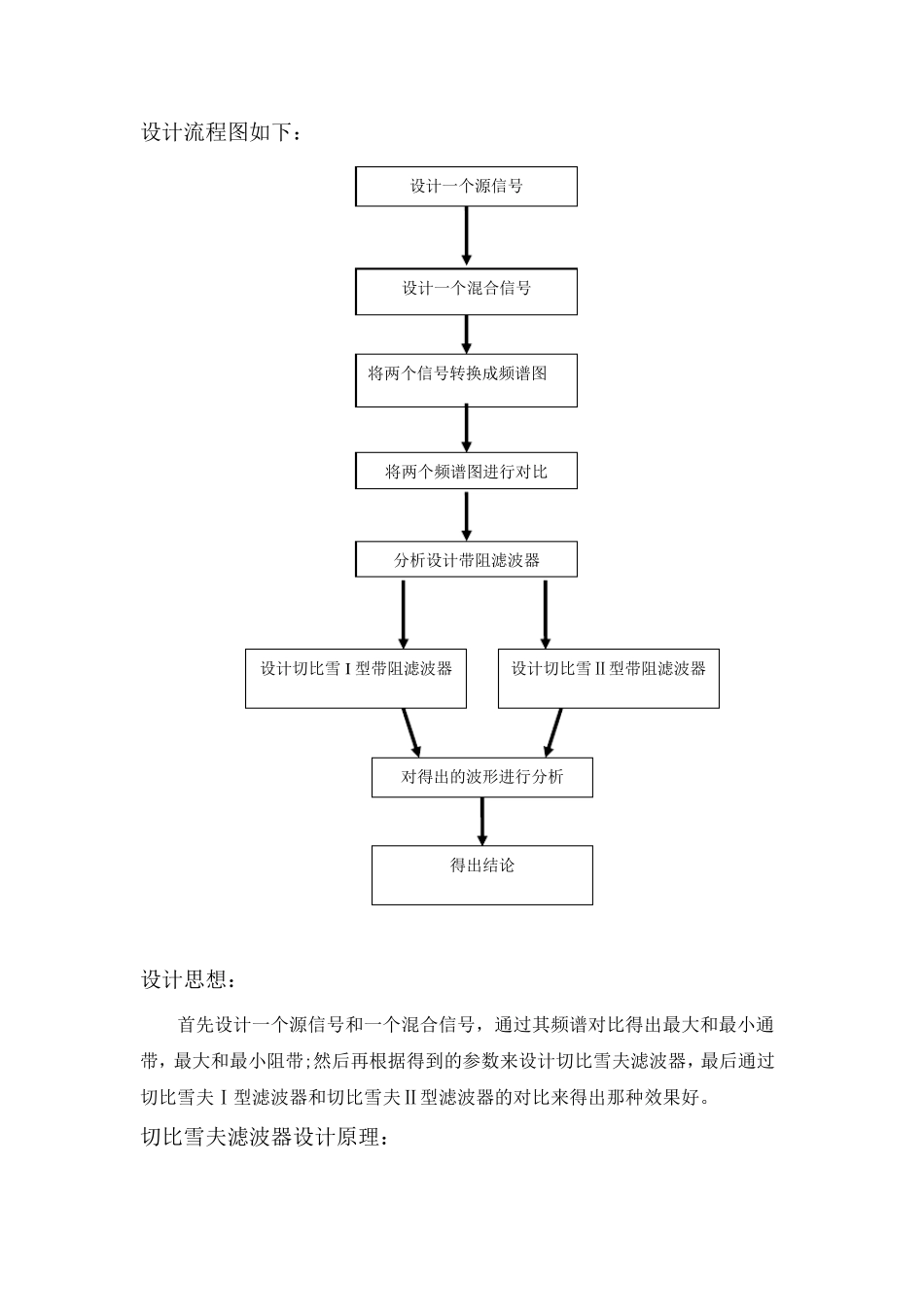
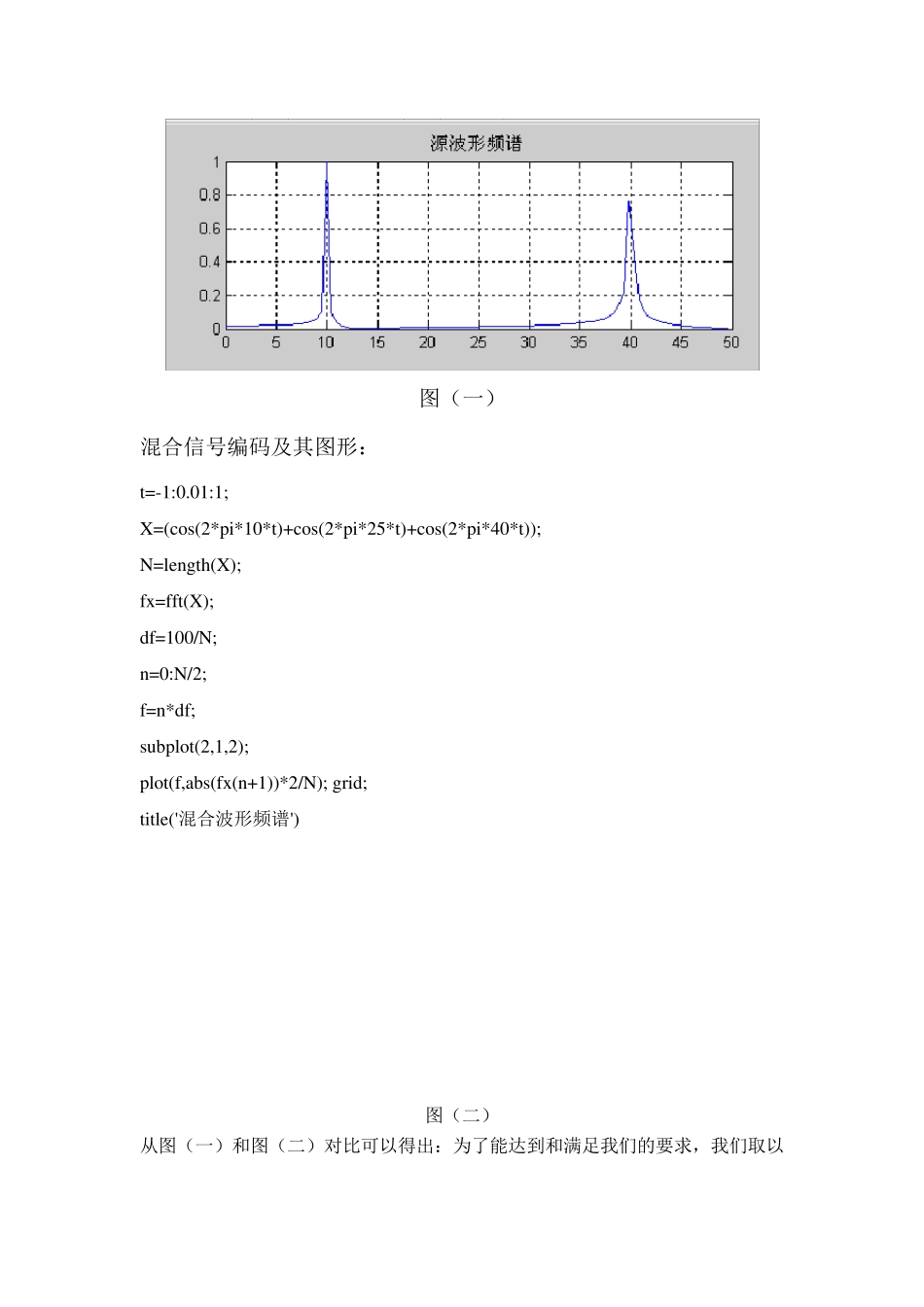
设计流程图如下: 设计思想: 首先设计一个源信号和一个混合信号,通过其频谱对比得出最大和最小通带,最大和最小阻带;然后再根据得到的参数来设计切比雪夫滤波器,最后通过切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比来得出那种效果好。 切比雪夫滤波器设计原理: 设计一个源信号 设计一个混合信号 将两个信号转换成频谱图 将两个频谱图进行对比 分析设计带阻滤波器 对得出的波形进行分析 设计切比雪I 型带阻滤波器 设计切比雪Ⅱ型带阻滤波器 得出结论 切比雪夫滤波器的振幅具有等波纹特性,它有两种形式:1)振幅特性在通带内是等波纹的、在阻带内是单调的切比雪夫I 型滤波器;2)振幅特性在通带内是单调的、在阻带内是等波纹的切比雪夫II型滤波器,采用何种形式的切比雪夫滤波器取决于实际用途. 切比雪夫滤波器的设计方法就是将逼近精确度均匀分布在整个通带内,或者均匀分布在整个阻带内,或者均匀分布在两者之内,这样就可以使滤波器阶数大大降低。 切比雪夫I型滤波器平方幅度响应函数表示为: 2)( jG=[1+2 C 2N ( )]2/1 其中 <1(正数),它与通带波纹有关, 越大,波纹也越大;CN ( ) 是切比雪夫多项式,它被定义为: CN ( )=cos(Narccos( )), ≤1, CN ( )=cosh(Narcosh( )), >1. 而切比雪夫II型滤波器平方幅度响应函数表示为: )( jG2 ={1+2 { C 2N ( )/[ 2N ( /c )] 2 }} 1 其中 <1(正数),表示波纹变化情况;c 为截止频率;N 为滤波器的阶次,也是 CN (N /) 的阶次。 源信号编码及其图形: t=-1:0.01:1 y=(cos(2*pi*10*t)+cos(2*pi*40*t)); N=length(y); fx=fft(y); df=100/N; n=0:N/2; f=n*df; subplot(2,1,1); plot(f,abs(fx(n+1))*2/N); grid; title('源波形频谱') 图(一) 混合信号编码及其图形: t=-1:0.01:1; X=(cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*40*t)); N=length(X); fx =fft(X); df=100/N; n=0:N/2; f=n*df; su bplot(2,1,2); plot(f,abs(fx (n+1))*2/N); grid; title('混合波形频谱') 图(二) 从图(一)和图(二)对比可以得出:为了能达到和满足我们的要求,我们取以下的参数,最大通带wp2:0.5,最小通带wp1:0.05,最大阻带ws2:0.3,最小阻带ws1:0.1。 切比雪夫Ⅰ型滤波器设计如下: ws1=0.1*pi;ws2=0.3*pi; %滤波器的阻带截止频率 wp1=0.05*pi;wp2=0.5...