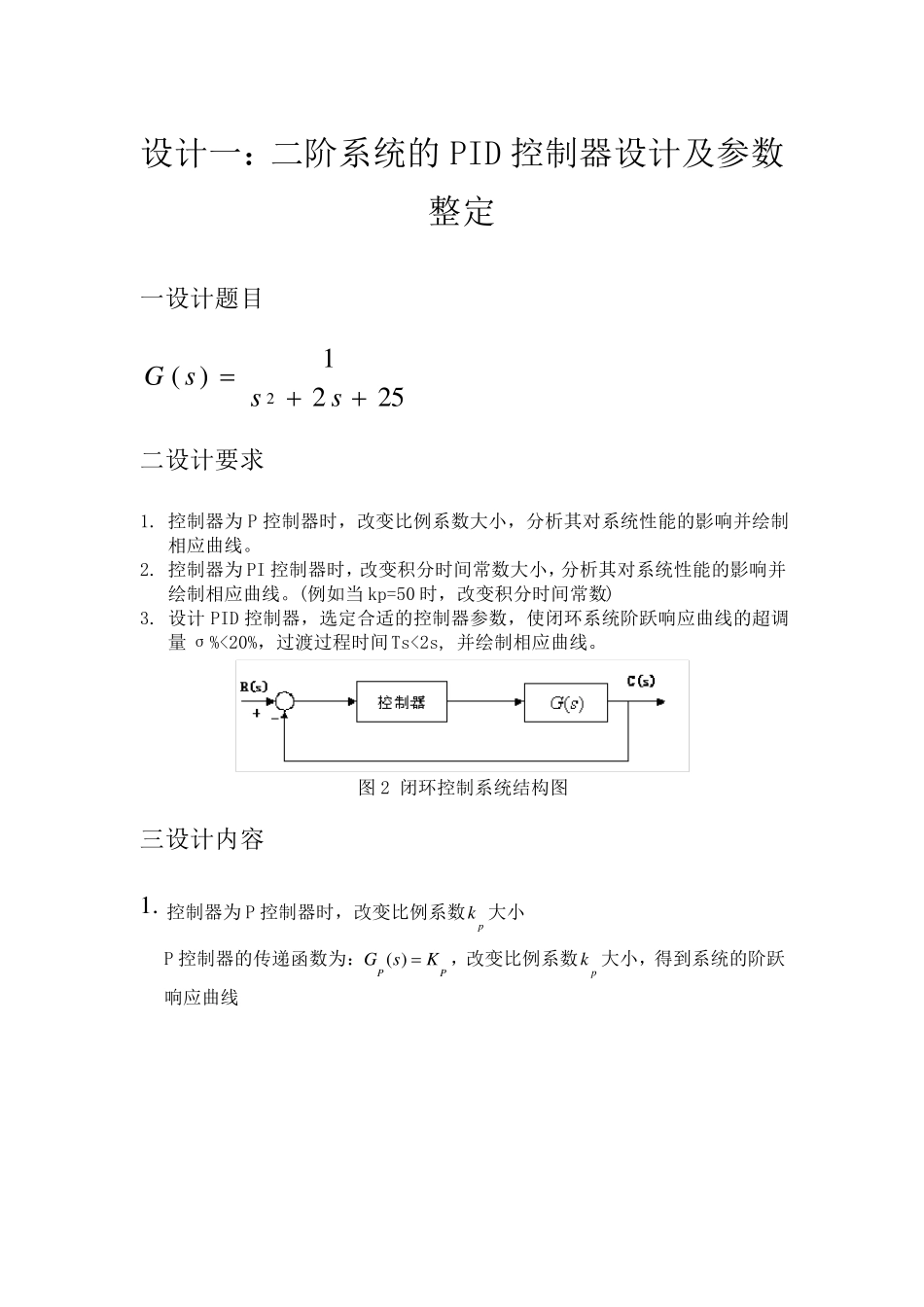
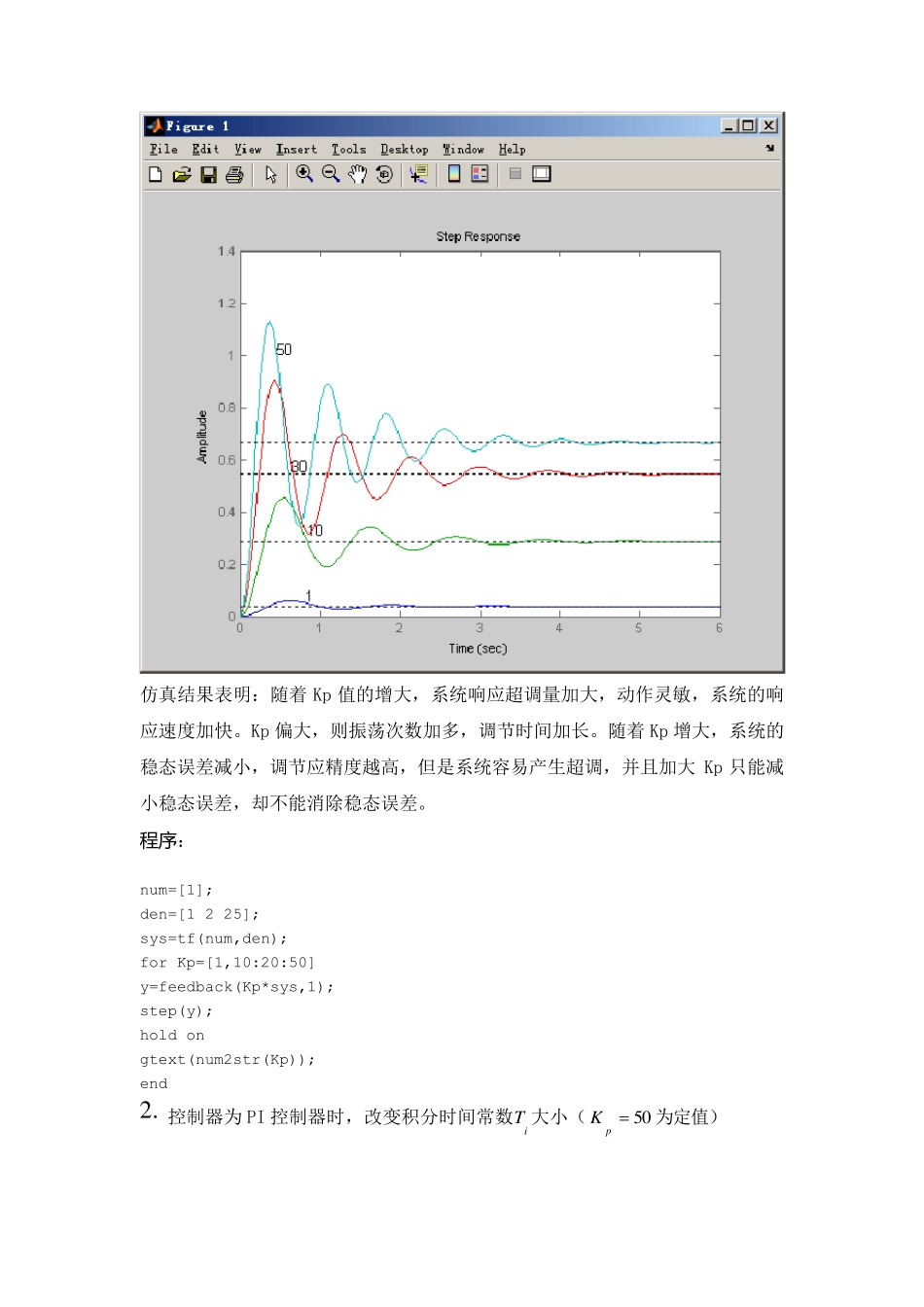
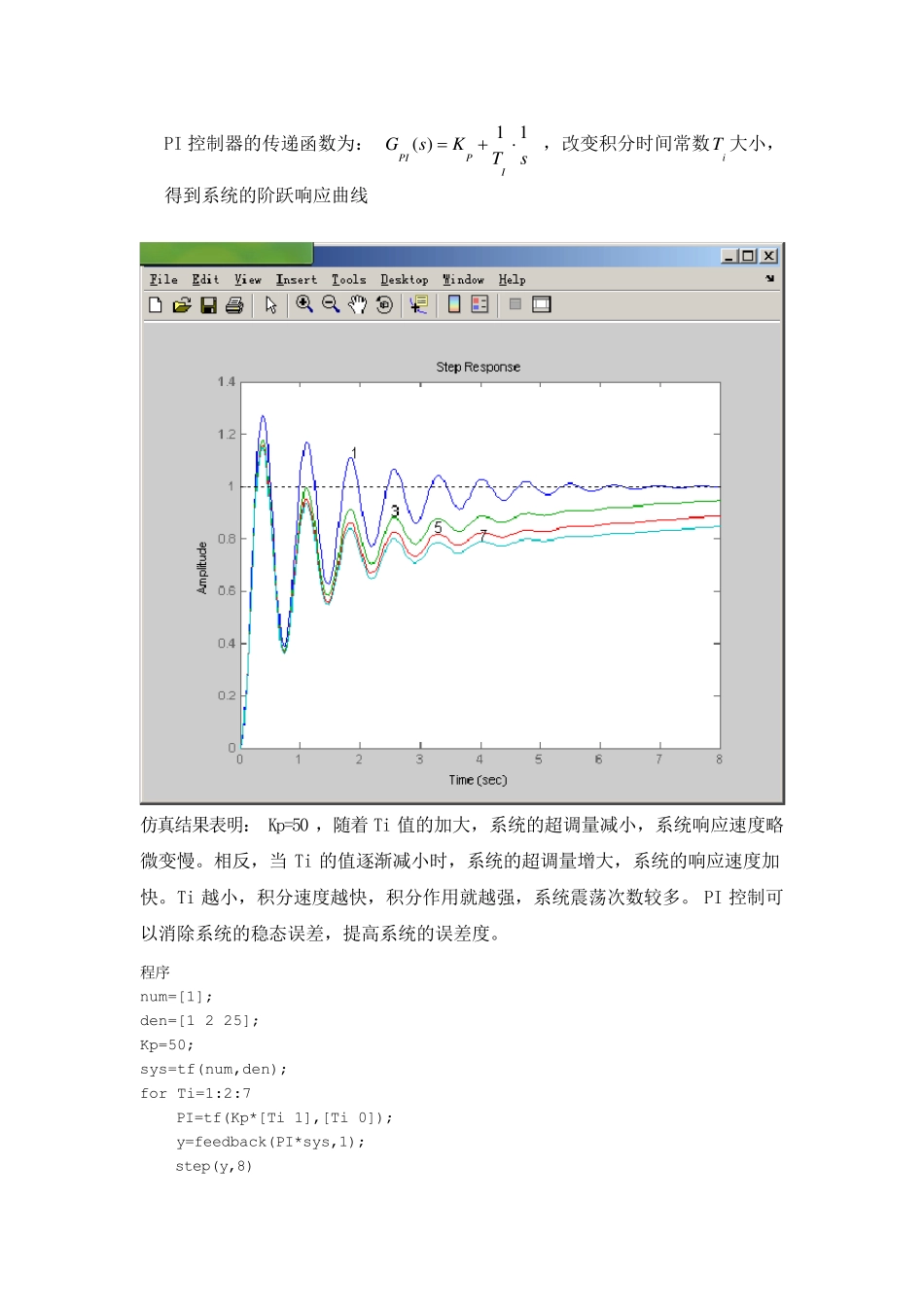
设计一:二阶系统的PID 控制器设计及参数整定 一设计题目 21( )22 5G sss 二设计要求 1. 控制器为P 控制器时,改变比例系数大小,分析其对系统性能的影响并绘制相应曲线。 2. 控制器为PI 控制器时,改变积分时间常数大小,分析其对系统性能的影响并绘制相应曲线。(例如当kp=50 时,改变积分时间常数) 3. 设计PID 控制器,选定合适的控制器参数,使闭环系统阶跃响应曲线的超调量σ%<20%,过渡过程时间Ts<2s, 并绘制相应曲线。 图 2 闭环控制系统结构图 三设计内容 1 . 控制器为P 控制器时,改变比例系数pk 大小 P 控制器的传递函数为:( )PPGsK,改变比例系数pk 大小,得到系统的阶跃响应曲线 仿真结果表明:随着Kp 值的增大,系统响应超调量加大,动作灵敏,系统的响应速度加快。Kp 偏大,则振荡次数加多,调节时间加长。随着Kp 增大,系统的稳态误差减小,调节应精度越高,但是系统容易产生超调,并且加大Kp 只能减小稳态误差,却不能消除稳态误差。 程 序 : num=[1]; den=[1 2 25]; sys=tf(num,den); for Kp=[1,10:20:50] y=feedback(Kp*sys,1); step(y); hold on gtext(num2str(Kp)); end 2 . 控制器为 PI 控制器时,改变积分时间常数iT 大小(5 0pK为定值) PI 控制器的传递函数为: 11( )PIPIGsKTs ,改变积分时间常数iT 大小,得到系统的阶跃响应曲线 仿真结果表明:Kp=50 ,随着Ti 值的加大,系统的超调量减小,系统响应速度略微变慢。相反,当 Ti 的值逐渐减小时,系统的超调量增大,系统的响应速度加快。Ti 越小,积分速度越快,积分作用就越强,系统震荡次数较多。 PI 控制可以消除系统的稳态误差,提高系统的误差度。 程序 num=[1]; den=[1 2 25]; Kp=50; sys=tf(num,den); for Ti=1:2:7 PI=tf(Kp*[Ti 1],[Ti 0]); y=feedback(PI*sys,1); step(y,8) hold on gtext(num2str(Ti)); end 3 . 控制器为PID 控制器时,改变微分时间常数dT 大小(5 0pK,1 5.0iT) PID 控制器的传递函数为:11( )PIDPDIGsKTsTs ,改变微分时间常数dT 大小,得到系统的阶跃响应曲线 仿真结果表明:Kp=50、Ti=0.15,随着 Td 值的增大,闭环系统的超调量减小,响应速度加快,调节时间和上升时间减小。加入微分控制后,相当于系统增加了零点并且加大了系统的阻尼比,提高了系统的稳定性和快速性。 程序 num=[1]; ...