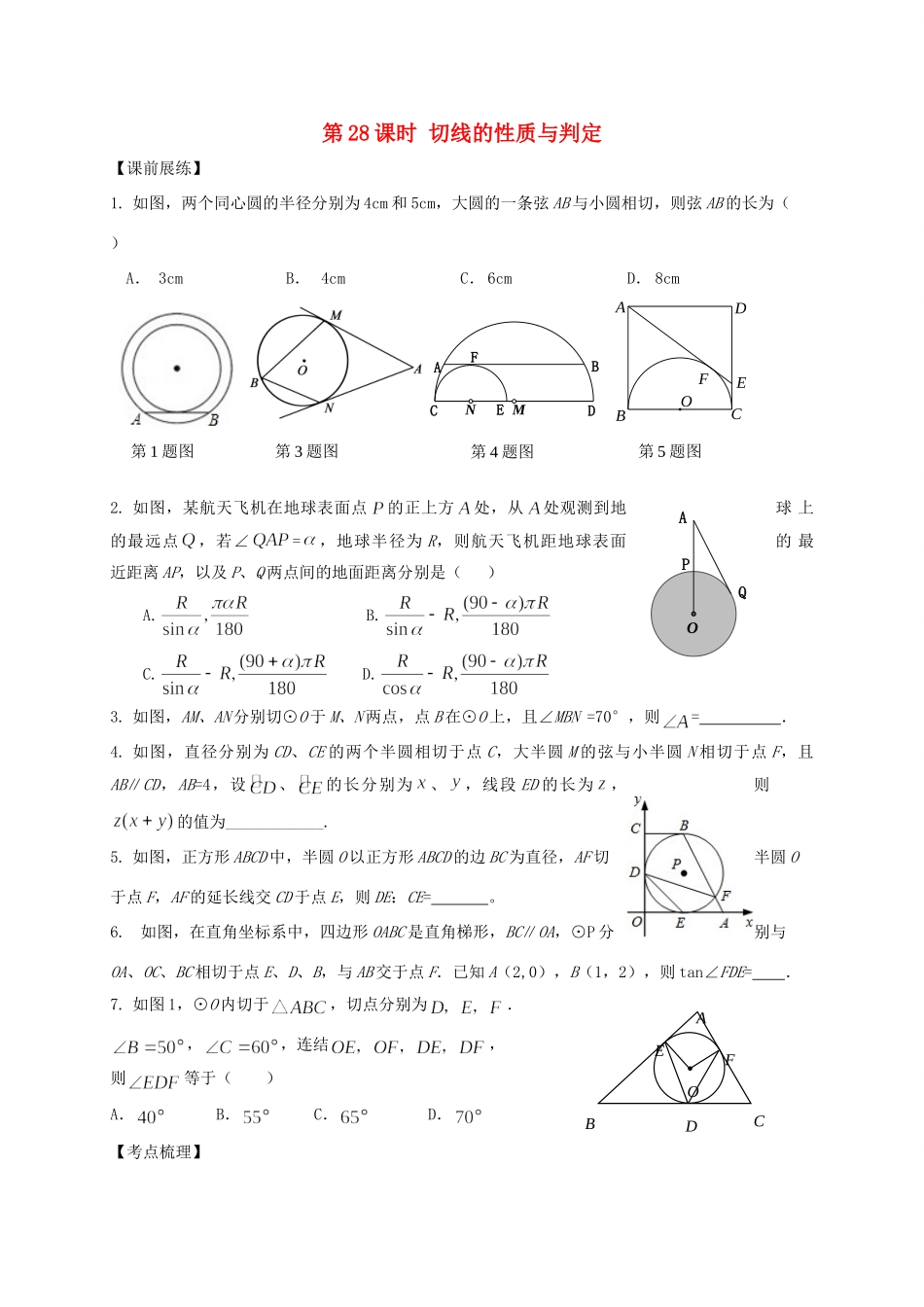
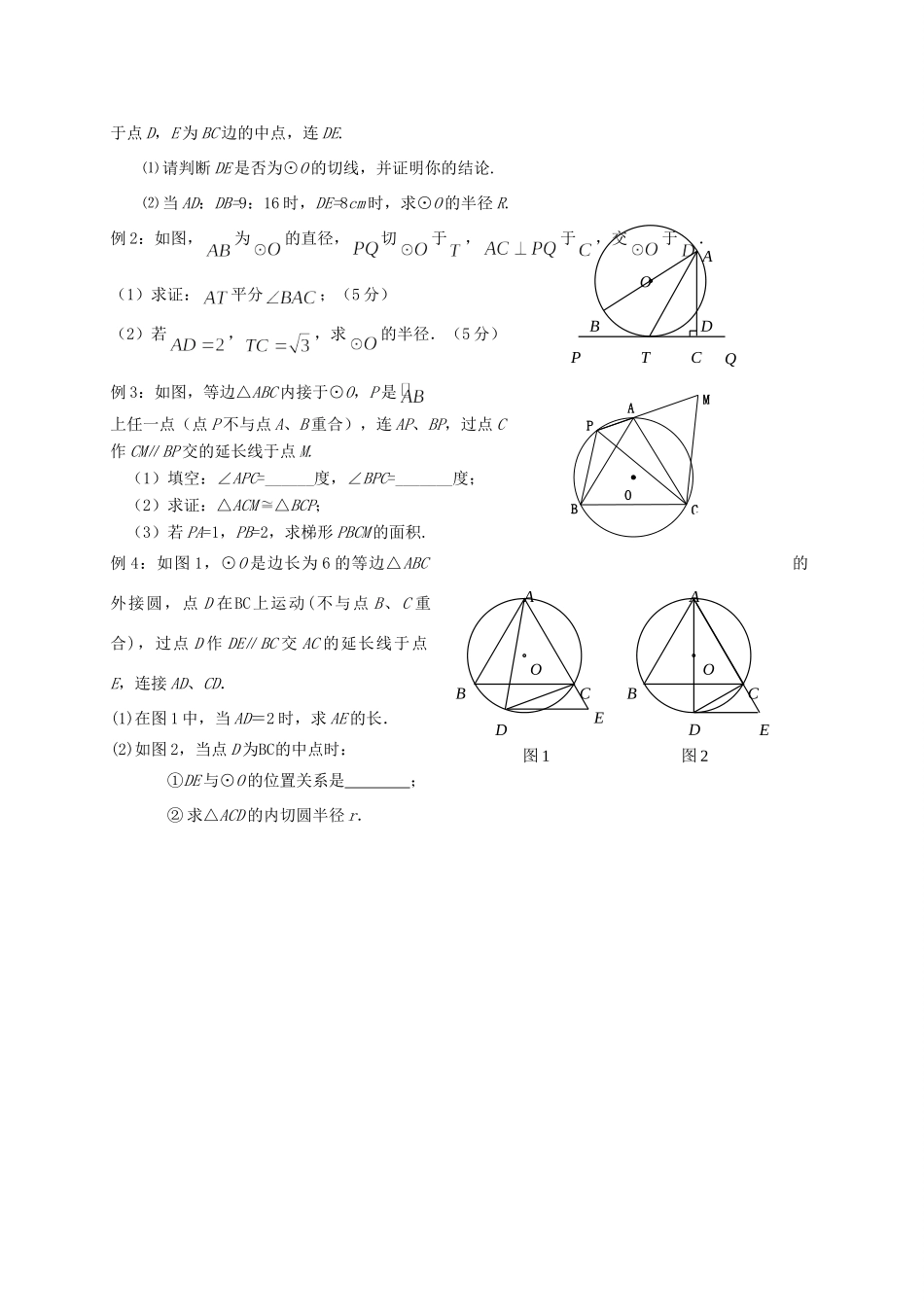
QPAO第 28 课时 切线的性质与判定【课前展练】1. 如图,两个同心圆的半径分别为 4cm 和 5cm,大圆的一条弦 AB 与小圆相切,则弦 AB 的长为( )A. 3cmB. 4cmC. 6cmD. 8cm2. 如图,某航天飞机在地球表面点的正上方处,从处观测到地球 上的最远点,若∠=,地球半径为 R,则航天飞机距地球表面的 最近距离 AP,以及 P、Q 两点间的地面距离分别是( ) A. B. C. D. 3. 如图,AM、AN 分别切⊙O 于 M、N 两点,点 B 在⊙O 上,且∠MBN =70°,则= .4. 如图,直径分别为 CD、CE 的两个半圆相切于点 C,大半圆 M 的弦与小半圆 N 相切于点 F,且AB∥CD,AB=4,设、的长分别为、,线段 ED 的长为,则的值为____________.5. 如图,正方形 ABCD 中,半圆 O 以正方形 ABCD 的边 BC 为直径,AF 切半圆 O于点 F,AF 的延长线交 CD 于点 E,则 DE:CE= 。6. 如图,在直角坐标系中,四边形 OABC 是直角梯形,BC∥OA,⊙P 分别与OA、OC、BC 相切于点 E、D、B,与 AB 交于点 F.已知 A(2,0),B(1,2),则 tan∠FDE= .7. 如图 1,⊙O 内切于,切点分别为.,,连结,则等于( )A. B. C. D.【考点梳理】第 1 题图第 3 题图DECFBANM第 4 题图FEODCBA第 5 题图DOAFCBE考点 1:切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定常用方法有三种:(1)和圆只有一个公共点的直线是圆的切线。(2)和圆心的距离等于圆的半径的直线是圆的切线。(3)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线辅助线的作法:证明一条直线是圆的切线的常用方法有两种:(1)当直线和圆有一个公共点时,把圆心和这个公共点连接起来,则得到半径,然后证明直线垂直于这条半径,记为“点已知,连半径,证垂直。”应用的是切线的判定定理。(2)当直线和圆的公共点没有明确时,过圆心作直线的垂线,再证圆心到直线的距离(d)等于半径(r),记为“点未知,作垂直,证半径”。应用的是切线的判定方法(2)。考点 2:切线的性质定理:圆的切线垂直于过切点的半径。辅助线的作法:有圆的切线时,常常连接圆心和切点得切线垂直半径。记为“见切线,连半径,得垂直。”考点 3:切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.对于切线长定理,应明确:(1)若已知圆的两条切线...