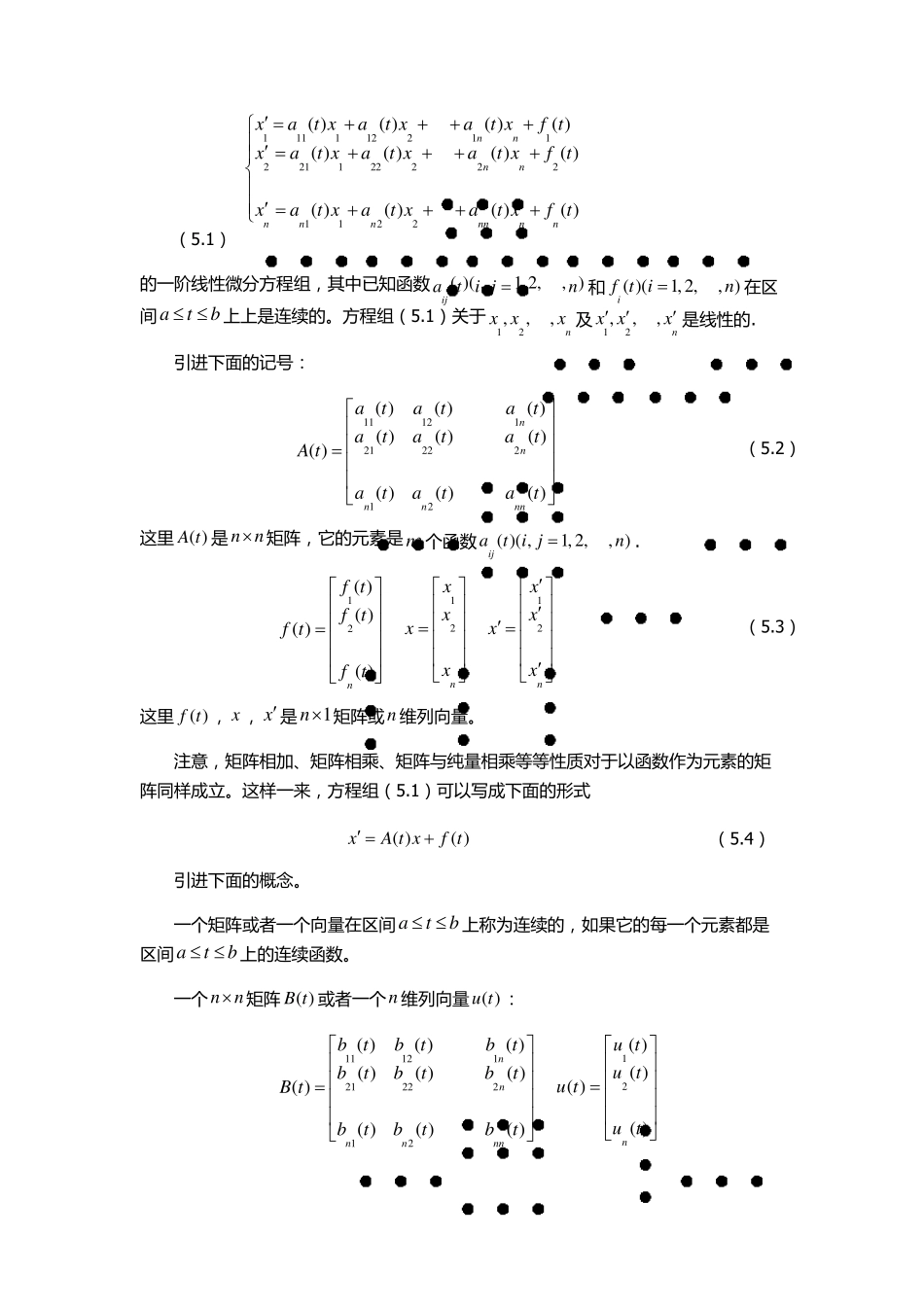
第 五 章 线 性 微 分 方 程 组 [教 学 目 标 ] 1. 理 解 线 性 微 分 方 程 组 解 的 存 在 唯 一 性 定 理 , 掌 握 一 阶 齐 ( 非 齐 ) 线 性 微 分 方 程 组 解的 性 质 与 结 构 , 2. 理 解 n 阶 线 性 微 分 方 程 与 一 阶 线 性 微 分 方 程 组 的 关 系 。 3. 掌 握 非 齐 次线 性 微 分 方 程 组 的 常数变易法, 4. 理 解 常系 数齐 线 性 微 分 方 程 组 基解 矩阵的 概念, 掌 握 求基解 矩阵的 方 法。 5. 掌 握 常系 数线 性 微 分 方 程 组 的 Laplce 变换法。 [教 学 中 难 点 ]求解 常系 数非 齐 次线 性 微 分 方 程 组 [教 学 方 法 ] 讲授, 实践。 [教 学 时 间 ] 16 学时 [教 学 内 容 ] n 阶 线 性 微 分 方 程 与 一 阶 线 性 微 分 方 程 组 的 关 系 , 一 阶 线 性 微 分 方 程 组 解的 存 在 唯 一 性 定 理 ;齐 ( 非 齐 ) 线 性 微 分 方 程 组 解 的 性 质 与 结 构 , 求解 非 齐 次线 性 微分 方 程 组 的 常数变易法;常系 数齐 线 性 微 分 方 程 组 的 基解 矩阵及求基解 矩阵的 方 法;求常系 数线 性 微 分 方 程 组 的 Laplce 变换法。 [考 核 目 标 ] 1.线 性 微 分 方 程 组 解 的 性 质 与 结 构 。 2.能够求解 常系 数线 性 微 分 方 程 组 。 §5.1 存 在 唯 一性 定理 5.1.1 记号和定义 考察形如 11 111 221122 112 22221122( )( )( )( )( )( )( )( )( )( )( )( )nnnnnnnnnnnxat xat xat xf txat xat xat xf txat xat xat xf t ( 5.1) 的 一 阶 线 性 微 分 方 程 组 , 其 中 已 知 函 数( )( ,1 , 2 ,, )ijat i jn和( )(1,2 ,, )if t in在 区间 atb 上 上 是 连 续 的 。 方 程 组 ( 5.1) 关 于12,,,nx xx 及12,,,nx xx 是 线 性 的 . 引 进 下 面 的 记 号 : 1 11 212 12 2212( )( )( )( )( )( )( )( )( )( )nnnnnnatatatatatatA tatatat ...