离散型随机变量的方差一VIP免费

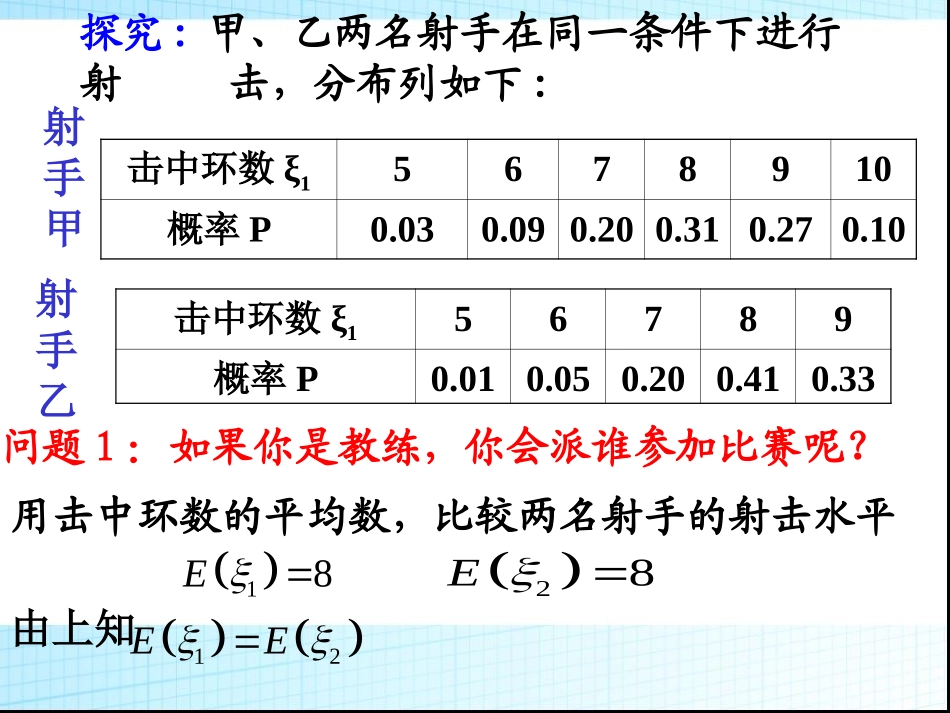
探究:甲、乙两名射手在同一条件下进行射击，分布列如下:击中环数ξ15678910概率P0.030.090.200.310.270.10射手甲射手乙击中环数ξ156789概率P0.010.050.200.410.33用击中环数的平均数，比较两名射手的射击水平由上知问题1：如果你是教练，你会派谁参加比赛呢？28E18E12EEpX1456789100.10.20.3(甲)X2456789100.10.20.30.4p(乙)思考：除平均中靶环数外，还有其他刻画两名同学各自射击特点的指标吗？2n22212)x(x)x(x)x(xn1s样本方差：n1)x(xn1)x(xn1)x(xs2n22212(x1-E(X))2·p1+(x2-E(X))2·p2+…+(xn-EX)2·pnD(X)=类似随机变量X的方差：称()()XDX为随机变量X的标准差。思考：怎样定量刻画随机变量的稳定性？思考：离散型随机变量的期望、方差与样本的期望、方差的区别和联系是什么？样本离散型随机变量均值公式意义方差或标准差公式意义nii=11x=xn1()iniiiEXxp随着不同样本值的变化而变化是一个常数随着不同样本值的变化而变化，刻画样本数据集中于样本平均值程度n1i2i2)x(xn1s)()nXEX2ii1D((x)是一个常数，反映随变量取值偏离均值的平均程度，D(X),越小，偏离程度越小.XD(ξ1)=D(ξ2)=由上知E(ξ1)=E(ξ2)，D(ξ1)>D(ξ2)例:甲、乙两名射手在同一条件下进行射击，分布列如下:击中环数ξ15678910概率P0.030.090.200.310.270.10射手甲射手乙击中环数ξ156789概率P0.010.050.200.410.33比较两名射手的射击水平E(ξ1)=8E(ξ2)=850.1)i(P)8i(105i1282.0)i(P)8i(95i22乙的射击成绩稳定性较好问题2：如果其他对手的射击成绩都在9环左右，应派哪一名选手参赛？问题3：如果其他对手的射击成绩都在7环左右，应派哪一名选手参赛？128,8EXEX121.50,0.82DXDX例1：随机抛掷一枚质地均匀的骰子，求向上一面的点数X的均值、方差和标准差。学以致用：例2：有甲乙两个单位都愿意聘用你，而你能获得如下信息：甲单位不同职位月工资X1/元1200140016001800获得相应职位的概率P10.40.30.20.1乙单位不同职位月工资X2/元1000140018002200获得相应职位的概率P20.40.30.20.1根据工资待遇的差异情况，你愿意选择哪家单位？解：121400,1400EXEX1240000,160000DXDX在两个单位工资的数学期望相等的情况下，如果认为自己能力很强，应选择工资方差大的单位，即乙单位；如果认为自己能力不强，就应选择工资方差小的单位，即甲单位。二、几个常用公式：2()DaXbaDX(1)XDXpp若服从两点分布，则~(,)(1)XBnpDXnpp若，则例3.篮球运动员在比赛中每次罚球命中率为p=0.6（1）求一次投篮时命中率次数X的期望与方差；（2）求重复5次投篮时，命中次数Y的期望与方差。一般地，若离散型随机变量X的概率分布列为……xnxi…x2x1Xpnpi…p2p1P三、课堂小结(x1-E(X))2·p1+(x2-E(X))2·p2+…+(xn-EX)2·pnD(X)=方差期望(1)()EaXbaEXb期望反映了X取值的平均水平。方差意义则E(X)=np2(1)()DaXbaDX（）(3)若X~B（n,p）则D(X)=np(1－p)计算公式(3)若X~B（n,p）(2)若X服从两点分布，则D(X)=p(1-p)方差反映了X取值的稳定与波动，集中与离散程度(2)若X服从两点分布,则E(X)=p相关练习：11313,8DD、已知，且则2(,)EX8,DX1.6,n,XBnpp_、已知～，则3、有一批数量很大的商品，其中次品占1％，现从中任意地连续取出200件商品，设其次品数为X，求E(X)和D(X)。117100.82，1.98课堂练习:24(()())DaXEXDX、等于（）2202()ABCaDXDaDXEX无法求5、已知随机变量X的分布列为：0.10.20.40.20.1P54321X另一随机变量Y=2X-3,求E（Y）,D（Y）1、离散型随机变量取值的方差、标准差及意义2、记住几个常见公式DXabaXD2)()1(ppDXX服从两点分布，则若)1(),(~pnpDXpnBX，则若例3、随机变量的分布列为其中，a,b,c成等差，若则的值为。-101Pabc1,3ED594.（08全国二18）购买某种保险，每个投保人每年度向保险公司交纳保费a元，若投...