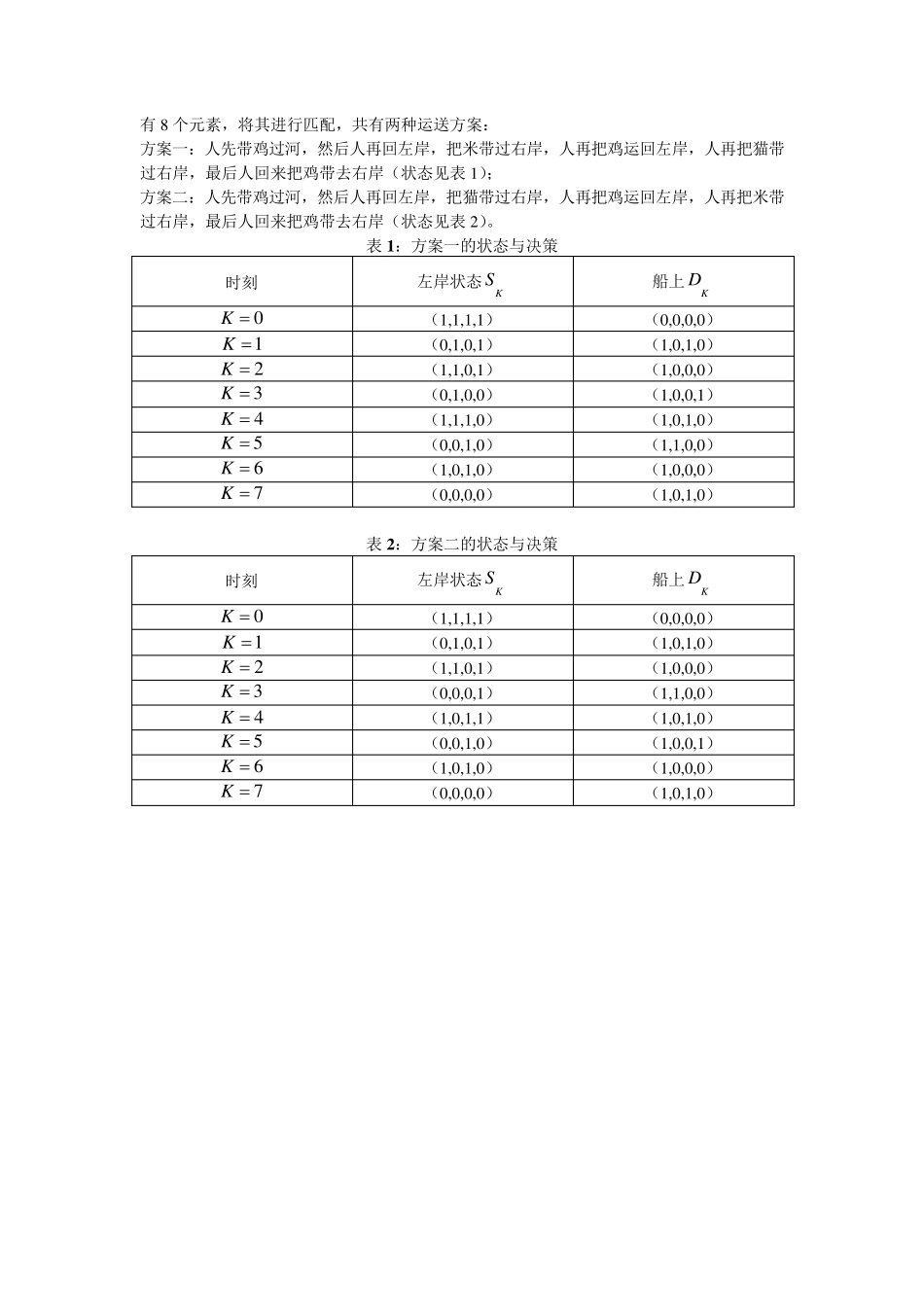
[习题1.4] 对长方形椅子在地面上可放稳的证明 问题背景 问题来自于书本1.3 案例一,椅子由正方形一般化为矩形。 建模准备 1. 椅子旋转方式:椅子四脚构成矩形ABCD,以垂直于平面ABCD,且经过对角线 AC,BD 交点 O 的直线为旋转轴;且旋转仅在平面ABCD 上进行; 2. ( ), ( )fg 意义同前;模型假设与 1.3 案例一相同。 模型建立与求解 ( )f 与 ( )g 均为连续函数。且由于任何时刻均有三脚着地,即( )f 与 ( )g 至少有一个为零,故( )( )0fg•恒成立。不失一般性,假设在初始时刻 AC 着地,即(0)0f。因此,对角线 BD 只要沿旋转轴旋转AOB即可保证BD 着地,不失一般性,可假设此时旋转角为2,(0)2(如图1),此时 ()02g ,()02f 。因此证明归结为证明以下数学命题: 已知( ), ( )fg 为连续函数,对任意(0, ),有( )( )0fg•;且(0)0f, (0)0g,()02g ,()02f ,(0,)2 ,0,s.t.00()()0fg. 证明:构造函数( )( )( )Ffg,易知( )F 连续 而(0)(0)(0)0Ffg 且()()()0222Ffg 由连续函数介值性定理,0(0,)2,0. . ()0s t F 且00000()()0()()()0fgFfg•00()()0fg 进一步研究 还有一种简便证明如下:按照上述旋转规则,椅子四脚在一个圆周上运动(如图二),假设椅子的D 脚一直不着地,则 ABC 三脚运动至 D 脚位置也会不着地,这与假设三矛盾,因此在圆周上必有一位置使得椅子四脚同时着地。 (图一,图二均在背面) [习题1.5] 人猫鸡米渡河问题研究 问题重述 人带着猫、鸡、米过河,从左岸到右岸,船除了需要人划之外,只能载猫、鸡、米三者之一,人不在场时猫要吃鸡、鸡要吃米。试设计一个安全过河方案,使渡河次数尽量地少。 符号说明 1X :代表人的状态,人在该左岸或船上取值为 1,否则为 0; 2X :代表猫的状态,猫在该左岸或船上取值为 1,否则为 0; 3X :代表鸡的状态,鸡在该左岸或船上取值为 1,否则为 0; 4X :代表米的状态,米在该左岸或船上取值为 1,否则为 0; 1234(,,,)KSXXXX:状态向量,代表时刻 K 左岸的状态; 1234(,,,)KDXXXX:决策向量,代表时刻 K 船上的状态; 模型的建立 状态向量集合412341...