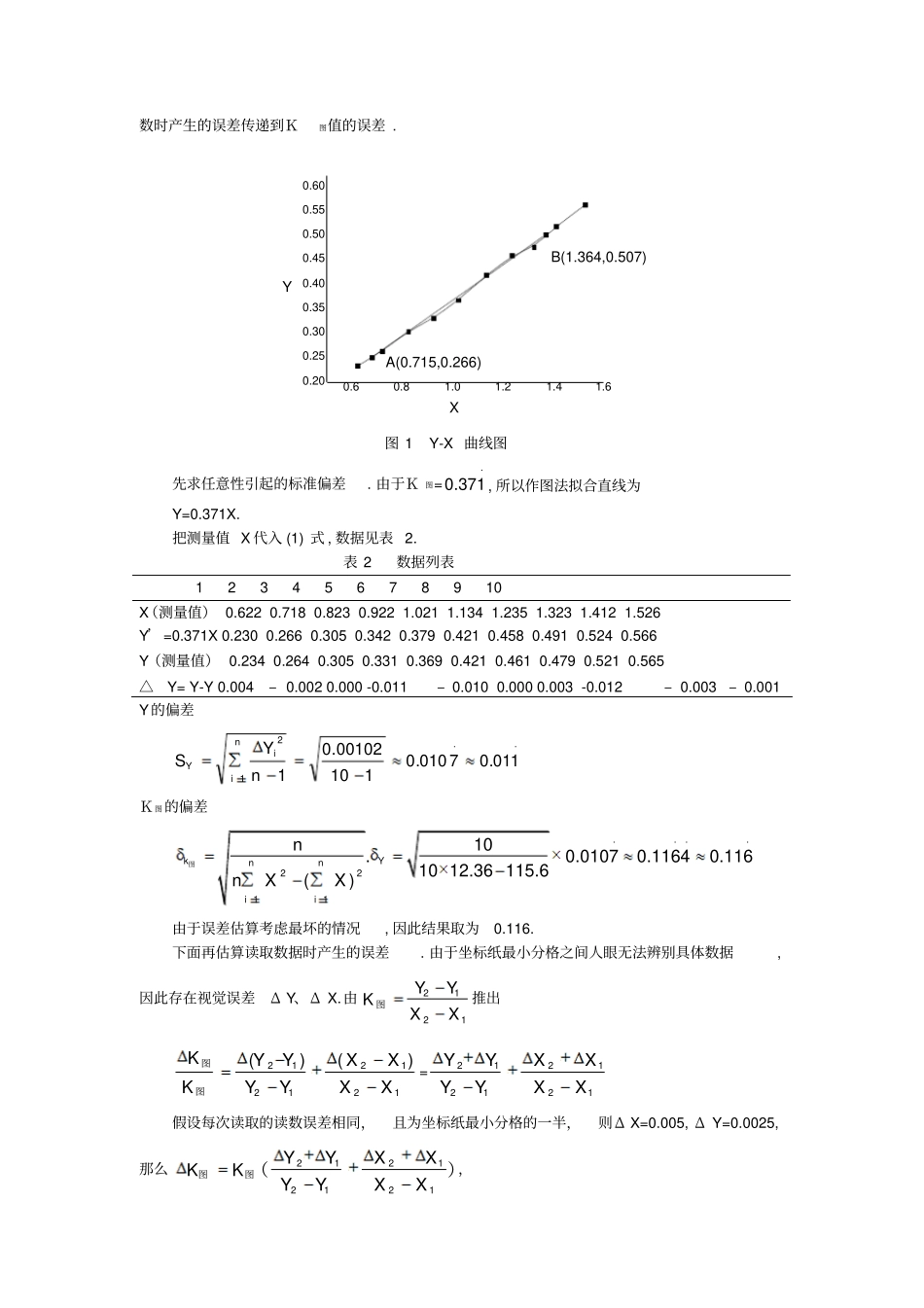
数值分析在化工中有限量测量数据处理方面的应用李刚辉((陕西科技大学化学与化工学院,陕西咸阳, 712081)摘要:介绍了插值法和最小二乘法两种数值分析方法在实验数据处理方面的具体应用;分析了数值分析方法在建立曲线拟合模型方面的应用。关键词:有限量测量数据;插值法;最小二乘法;曲线拟合定量分析的目的是通过实验测定试样中被测组分的准确含量。但由于受分析方法、测量仪器、试剂和分析人员主客观因素等方面的限制,使测量结果不可能与真实结果完全一致;同时, 一个定量分析往往要经过一系列步骤,并不是一次简单的测量,每步测量的误差都会影响分析结果的准确性。因此, 即使是技术娴熟的技术人员,用各项技术指标均符合要求的测量仪器, 用同一种可靠方法对同一试样进行多次测量,也不能得到完全一致的结果。这说明客观上存在着难以避免的误差,任何测量结果都不可能绝对准确。为了提高分析的准确性,有必要探讨产生误差的原因和减免误差的方法。由于误差的客观存在,人们在实际分析中不可能得到确切无误的真实值,而需对测量结果作出相对准确的估计。如何得到最佳的估计值并判断其可靠性,这是对测量数据进行数值分析的目的。另外,在分析测量中,由于各种误差的存在,两个变量间一般不存在确切的函数关系,而仅是相关关系。 在进行两变量间的相关分析时,最直观的方法是建立直角坐标系,两个变量各占一坐标轴, 每个数据在坐标系中为一个点,并将数据连接成一条直线或曲线以显示变量间的相互关系。 如各点的连接排列接近一条直线,则表明两变量的线性相关性较好;如各点排列杂乱无章, 则表明两变量的线性相关性较差。但仅凭目测配线是不够准确的,不同的人对同一数据会给出不同的配线。较好的方法是对数据进行模拟,求出曲线模拟方程。本文介绍了插值法和最小二乘法两种数值分析方法在实验数据处理方面的具体应用,并分析了数值分析方法在建立曲线拟合模型方面的应用。1 数值分析法在实验数据处理方面的具体应用1.1 作图法和最小二乘法在实验数据处理方面的具体应用以一化学实验为例子,其公式为Y=KX 。测量数据见表1,其中“ .”表示估读数字。下面分析其两种方法处理数据之后的有效数字情况。表 1 数据列表物理量1 2 3 4 5 6 7 8 9 10 X .262.0.871.0.382.0.292.0.1.021.1.134.1.235.1.323.1.412.1.526Y .0.234.0.264.0.305.0.331.0.369.0.421.0.461.0.479.0.521.0.5651.1.1 作图法用表 1 中数据组...