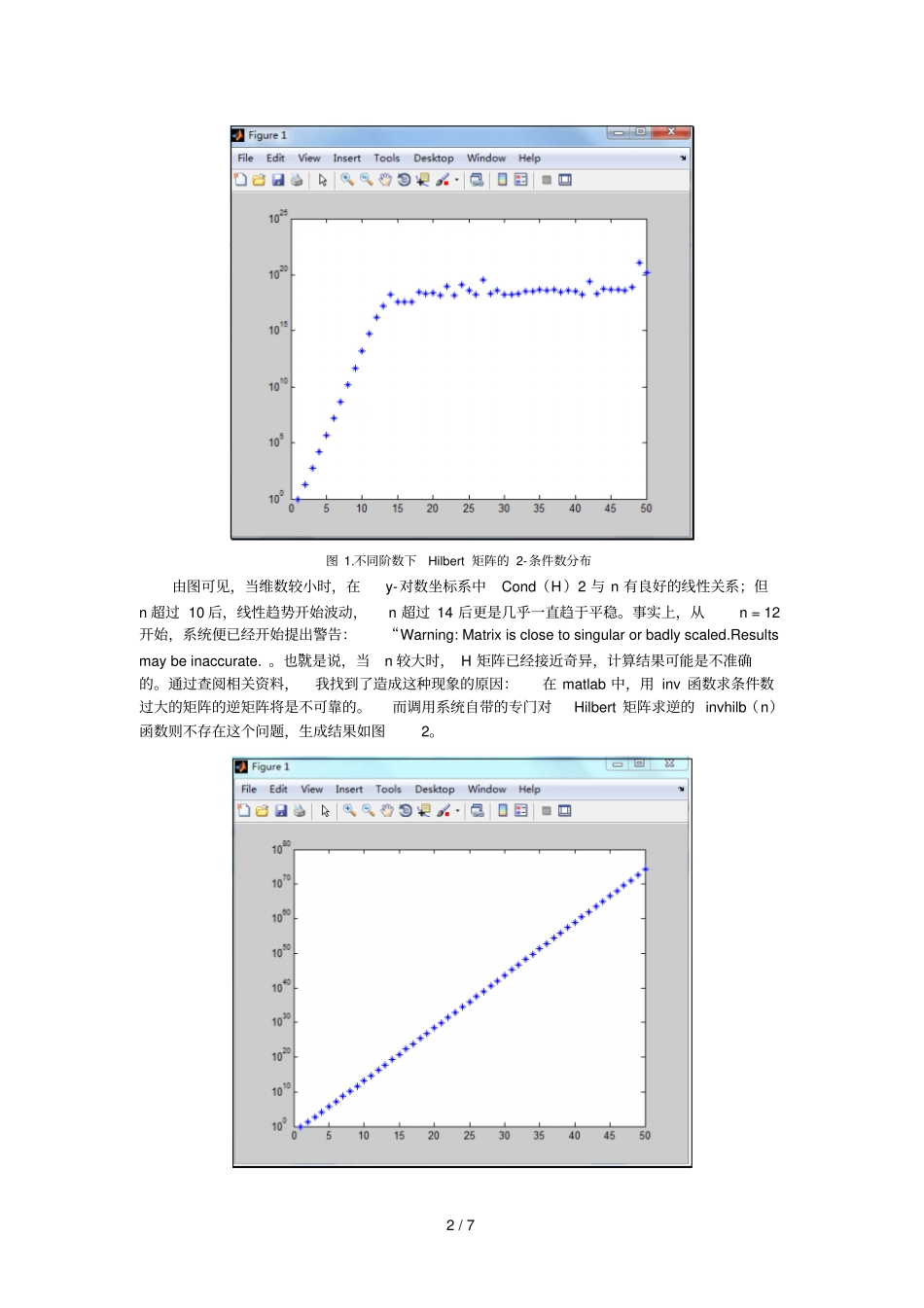
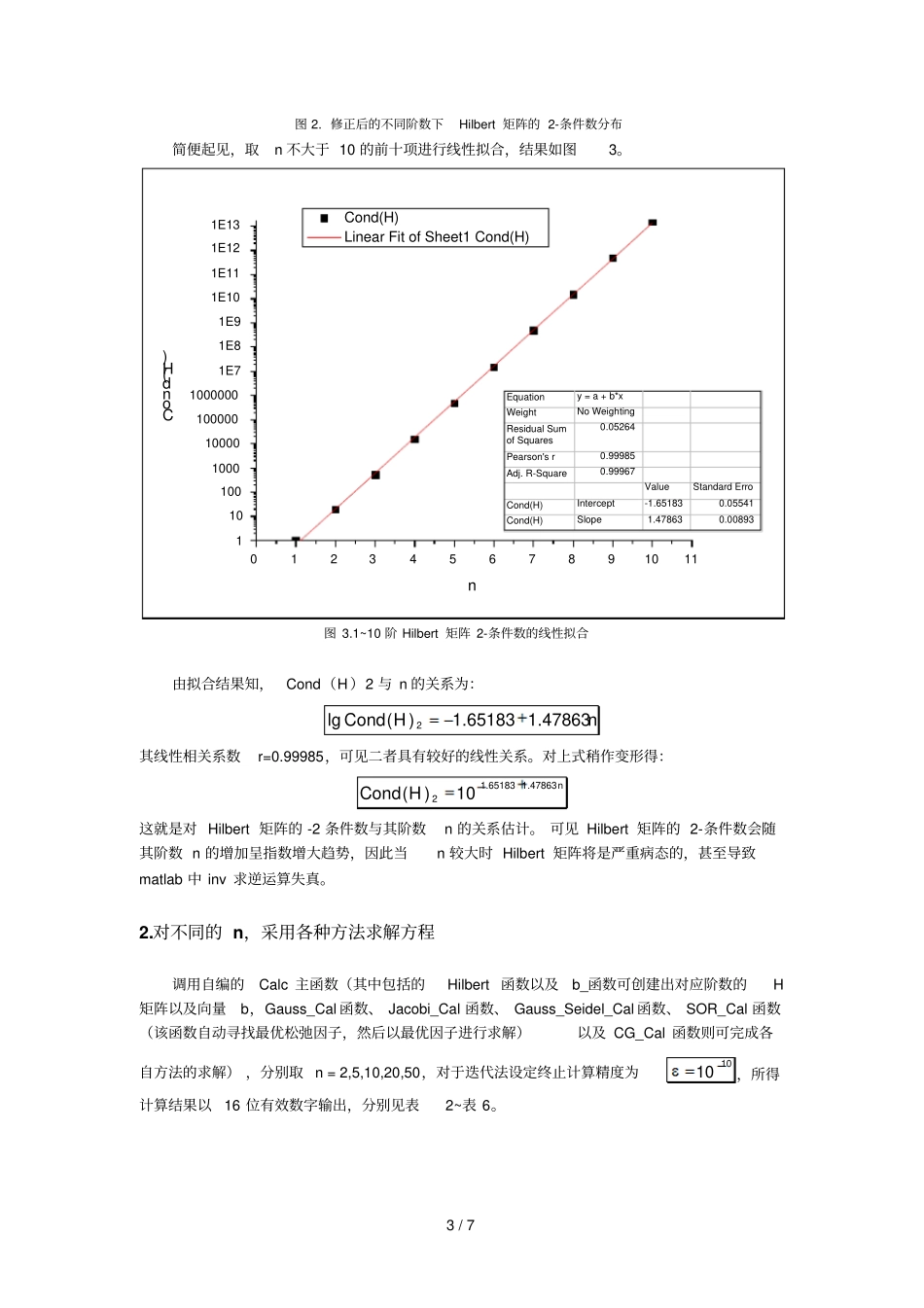
1 / 7 数值分析课程实验报告题目:病态线性方程组的求解理论分析表明,数值求解病态线性方程组很困难。考虑求解如下的线性方程组的求解Hx = b,期中 H 是 Hilbert 矩阵,()ijn nHh,11ijhij, i,j = 1,2 ,⋯,n 1.估计矩阵的2 条件数和阶数的关系2.对不同的 n,取(1,1,,1)nx,分别用Gauss 消去, Jacobi 迭代, Gauss-seidel 迭代, SOR 迭代和共轭梯度法求解,比较结果。3.结合计算结果,试讨论病态线性方程组的求解。解答过程1.估计矩阵的 2-条件数和阶数的关系矩阵的 2-条件数定义为:1222()Cond AAA,将 Hilbert 矩阵带入有:1222()Cond HHH调用自编的Hilbert_Cond 函数对其进行计算,取阶数n = 50,可得从 1 阶到 50 阶的 2-条件数,以五位有效数字输出,其中前10 项见表 1。表 1.前十阶 Hilbert 矩阵的 2-条件数阶数1 2 3 4 5 2-条件数1 19.281 524.06 1.5514e+004 4.7661e+005 阶数6 7 8 9 10 2-条件数1.4951e+007 4.7537e+008 1.5258e+010 4.9315e+011 1.6025e+013 从表 1 可以看出,随着阶数每递增1,Hilbert 矩阵的 2-条件数都至少增加一个数量级,但难以观察出明显的相依规律。故考虑将这些数据点绘制在以n 为横轴、 Cond( H) 2 为纵轴的对数坐标系中(编程用Hilbert_Cond 函数同时完成了这个功能),生成结果如图1。2 / 7 图 1.不同阶数下Hilbert 矩阵的 2-条件数分布由图可见,当维数较小时,在y-对数坐标系中Cond(H)2 与 n 有良好的线性关系;但n 超过 10 后,线性趋势开始波动,n 超过 14 后更是几乎一直趋于平稳。事实上,从n = 12开始,系统便已经开始提出警告:“Warning: Matrix is close to singular or badly scaled.Results may be inaccurate.”。也就是说,当n 较大时, H 矩阵已经接近奇异,计算结果可能是不准确的。通过查阅相关资料,我找到了造成这种现象的原因:在 matlab 中,用 inv 函数求条件数过大的矩阵的逆矩阵将是不可靠的。而调用系统自带的专门对Hilbert 矩阵求逆的 invhilb(n)函数则不存在这个问题,生成结果如图2。3 / 7 图 2. 修正后的不同阶数下Hilbert 矩阵的 2-条件数分布简便起见,取n 不大于 10 的前十项进行线性拟合,结果如图3。0123456789101111010010001000010000010000001E71E81E91E101E111E121E13 Cond(H) Linear Fit of Sheet1 Cond(H)Cond(H)nEq...