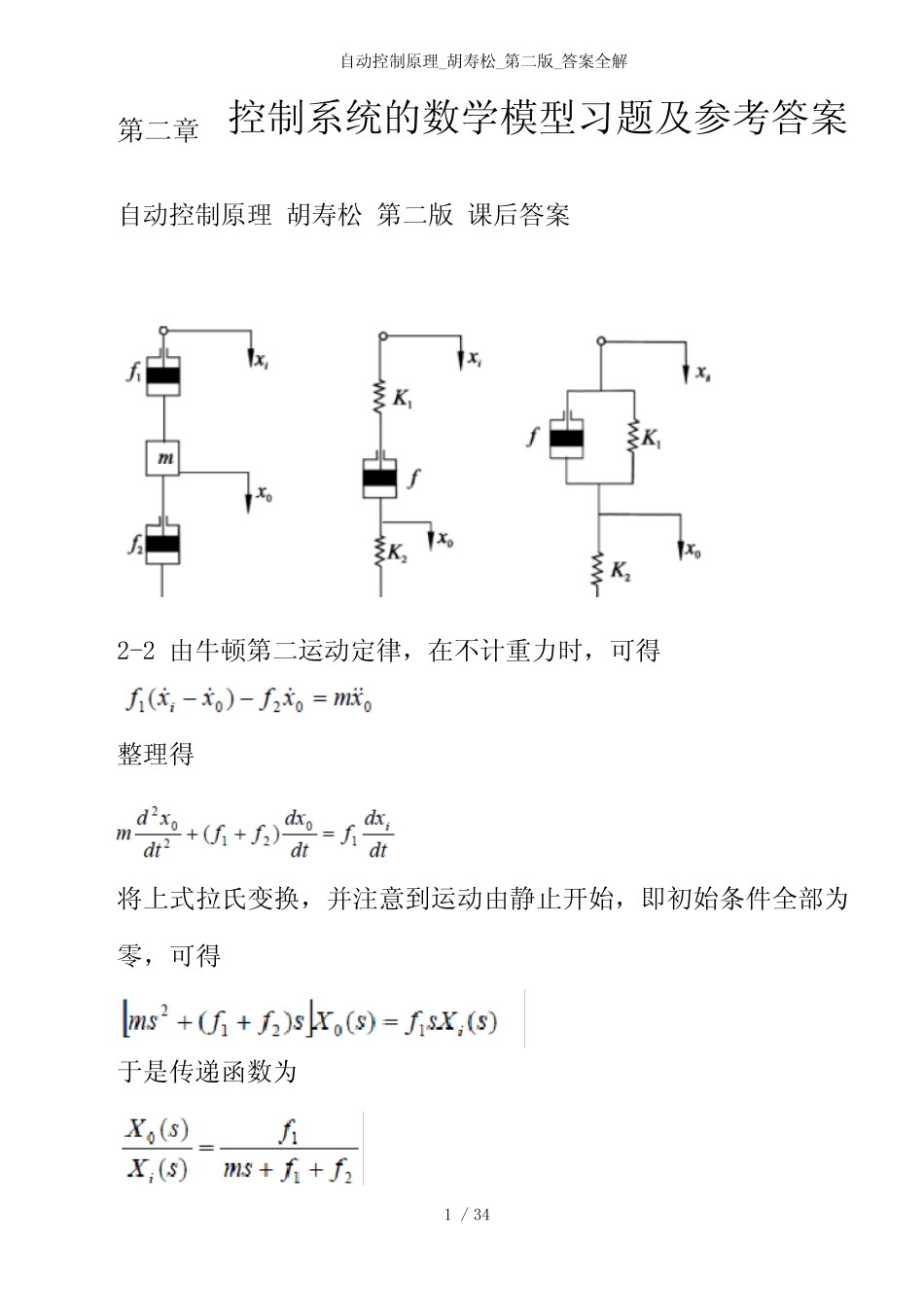
自 动 控 制 原 理 _胡 寿 松 _第 二 版 _答 案 全 解 1 / 34 第 二 章 控 制 系 统 的 数 学 模 型 习 题 及 参 考 答 案 自 动 控 制 原 理 胡 寿 松 第 二 版 课 后 答 案 2-2 由 牛 顿 第 二 运 动 定 律 , 在 不 计 重 力 时 , 可 得 整 理 得 将 上 式 拉 氏 变 换 , 并 注 意 到 运 动 由 静 止 开 始 , 即 初 始 条 件 全 部 为零 , 可 得 于 是 传 递 函 数 为 自 动 控 制 原 理 _胡 寿 松 _第 二 版 _答 案 全 解 2 / 34 ② 其 上 半 部 弹 簧 与 阻 尼 器 之 间 , 取 辅 助 点 A, 并 设 A点 位 移 为 x,方 向 朝 下 ; 而 在 其 下 半 部 工 。 引 出 点 处 取 为 辅 助 点 B。 则 由 弹 簧 力与 阻 尼 力 平 衡 的 原 则 , 从 A和 B两 点 可 以 分 别 列 出 如 下 原 始 方 程 : 消 去 中 间 变 量 x, 可 得 系 统 微 分 方 程 对 上 式 取 拉 氏 变 换 , 并 计 及 初 始 条 件 为 零 , 得 系 统 传 递 函 数 为 ③ 以 引 出 点 作 为 辅 助 点 , 根 据 力 的 平 衡 原 则 , 可 列 出 如 下 原 始 方程 : 移 项 整 理 得 系 统 微 分 方 程 对 上 式 进 行 拉 氏 变 换 , 并 注 意 到 运 动 由 静 止 开 始 , 即 则 系 统 传 递 函 数 为 自 动 控 制 原 理 _胡 寿 松 _第 二 版 _答 案 全 解 3 / 34 2-3 (b)以 k1 和 f1 之 间 取 辅 助 点 A, 并 设 A 点 位 移 为 x, 方 向 朝 下 ;根 据 力 的 平 衡 原 则 , 可 列 出 如 下 原 始 方 程 : 自 动 控 制 原 理 _胡 寿 松 _第 二 版 _答 案 全 解 4 / 34 所 以 2-6 解 : 自 动 控 制 原 理 _胡 寿 松 _第 二 版 _答 案 全 解 5 / 34 2-7 解 : 2-8 解 : 自 动 控 制 原 理 _胡 寿 松 _第 二 版 _答 案 全 解 6 / 34 2-9 解 : 自 动 控 制 原 理 _胡 寿 松 _第 二 版 _答 案 全 解 7 / 34 2-10 解 : 系 统 的 结 构 图 如 下 : ...