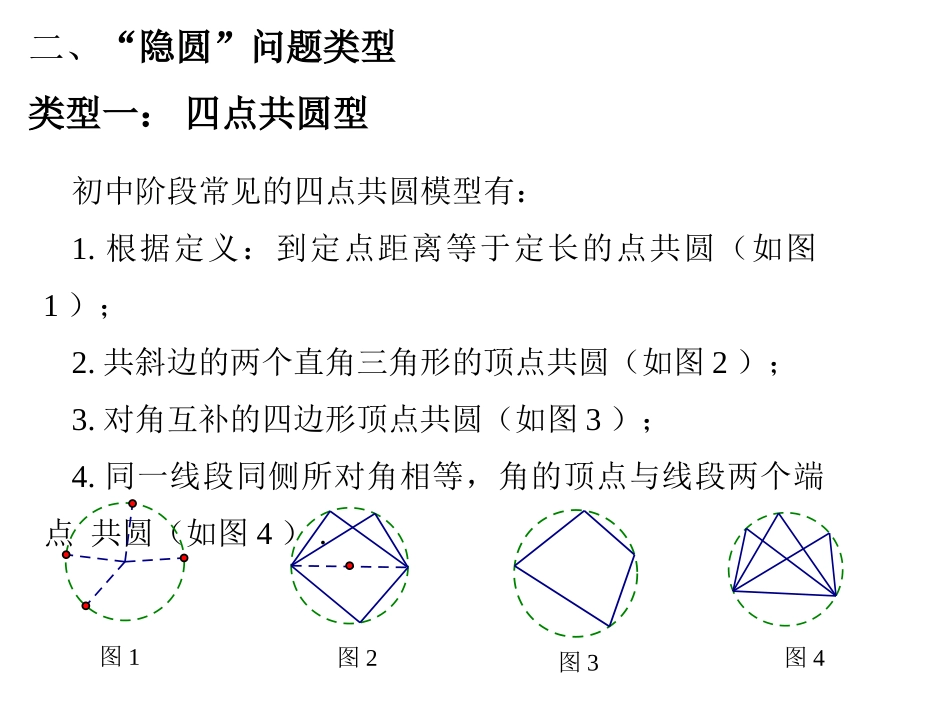
第51课时“隐圆”问题一、专题解读1.近年来全国各省市中考试题,圆的考查形式往往有两种:一种是题干中给出圆,以圆为背景命制试题;另一种是题设中没有圆,但在解题过程中,需要构造圆,利用圆的相关知识来解决问题.我们称第二种为“隐圆”问题;2.广州市2018年第25题、2019年第24题,均考到“隐圆”问题;3.本专题可安排两个课时.二、“隐圆”问题类型类型一:四点共圆型初中阶段常见的四点共圆模型有:1.根据定义:到定点距离等于定长的点共圆(如图1);2.共斜边的两个直角三角形的顶点共圆(如图2);3.对角互补的四边形顶点共圆(如图3);4.同一线段同侧所对角相等,角的顶点与线段两个端点共圆(如图4).图1图2图3图4典例解析1.(2014天河区二模)如图5,坐标原点O在线段AC上,点D,E在AC同侧,,,AD=OC=3,CE=6.点P为线段AO上的动点,连接DP,作,交直线OE与点Q;90DACECAoODOEDPPQCOQEPDAxy图5(1)求D、E的坐标;D(-6,3),E(3,6)(2)当点P与,O两点不重合时,求的值;DPPQA连结DQ OD⊥OE,DP⊥PQ,∴∠DPQ=∠DBQ=90°,∴点D、P、O、Q都在以DQ为直径的圆上,∴∠DQP=∠DOA, tan∠DQP=tan∠DOA,∴中考演练(一)1.(2020沈阳市第25题第1问)如图6,射线AB和射线CB相交于点B,∠ABC=α(0°<α<180°),且AB=CB.点D是射线CB上的动点(点D不与点C和点B重合),作射线AD,并在射线AD上取一点E,使∠AEC=α,连接CE,BE,当点D在线段CB上,α=90°时,请直接写出∠AEB的度数=;EDBCA图645°易证A、B、E、C四点共圆,△ABC是等腰直角三角形,则∠ACB=45°,∴∠AEB=∠ACB=45°.2.(2020番禺一模)如图7,长为定值的弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),点E是CD的中点,过点C作CF⊥AB于F,若CD=3,AB=8,则EF的最大值是().OBFEADC图7A.B.C.D.924836B3.(2020四川甘孜州第27题第2问)如图7,Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点D落在线段AB上,连接BE.试判断BE与AB的位置关系,并说明理由.图7由旋转的性质可知,∠DBC=∠CED,∴D、C,E,B四点共圆, ∠DCE=90°,∴∠DBE=90°,∴BE⊥AB.4.(2020临沂第26题第3问)如图8,菱形ABCD的边长为1,∠ABC=60°,点E是边AB上任意一点(端点除外),线段CE的垂直平分线交BD、CE分别于点F、G.线段AE、EF的中点分别为M、N.当点E在AB上运动时,∠CEF的大小是否变化?为什么?GNFEBDCMA图8如图1,分别连接MG、AC、FM,则MG∥AC,∠GME=∠CAB=∠ABC=60°;易证FC=FA=FE则NG=FN=EN=MN,∴点F、M、E、G在以N为圆心,EF为直径的圆上,∴∠CEF=∠FMG=90°-∠GME=30°,即∠CEF的大小无变化.GNFEBDCMA图1类型二:路径(轨迹)为圆(弧)型典例解析2.点A与点B的坐标分别是(1,0)、(5,0),点P是该直角坐标系内的一个动点,且满足∠APB=30°.(1)画出点P的路径图;以AB为边,在第一象限内作等边△ABC,以点C为圆心,AC为半径作⊙C,交y轴于点P1、P2.优弧AP1B即为点P的路径.(2)当点P在y轴正半轴时,求点P的坐标.中考演练(二)5.(2020山东泰安第12题)如图10,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC1﹦,点M为线段AC的中点,连接OM,则OM的最大值为()MxyOBCA图10B6.(2019武汉)如图11,AB是⊙O的直径,M、N是弧AB(异于A、B)上两点,C是弧MN上一动点,∠ACB的角平分线交⊙O于点D,∠BAC的平分线交CD于点E.当点C从点M运动到点N时,C、E两点的运动路径长的比是()BNODMAC图11A类型三:定角对定弦型典例解析3.(2020广西北部湾第18题)如图12,在边长为的菱形ABCD中,∠C=60°,点E,F分别是AB,AD上的动点,且AE=DF,DE与BF交于点P.当点E从点A运动到点B时,点P的运动路径长为.23图12如图3,点E,F在AB,AD上运动的过程中,DE、BF相交所成的∠BPD始终保持不变,为120°,连结BD,易知BD=,此时B,C,D,P四点共圆,点P的运动的路径的长即为.图3中考演练(三)7.如图13,线段BC的两个端点分别在x轴与直线上滑动(均不与原点O重合),且BC=2,分别作BP⊥x轴,CP⊥OC,交点为P,设点P坐标为(m,n),则=.3yx22mnPxyO...