系统辨识之最小二乘法VIP免费

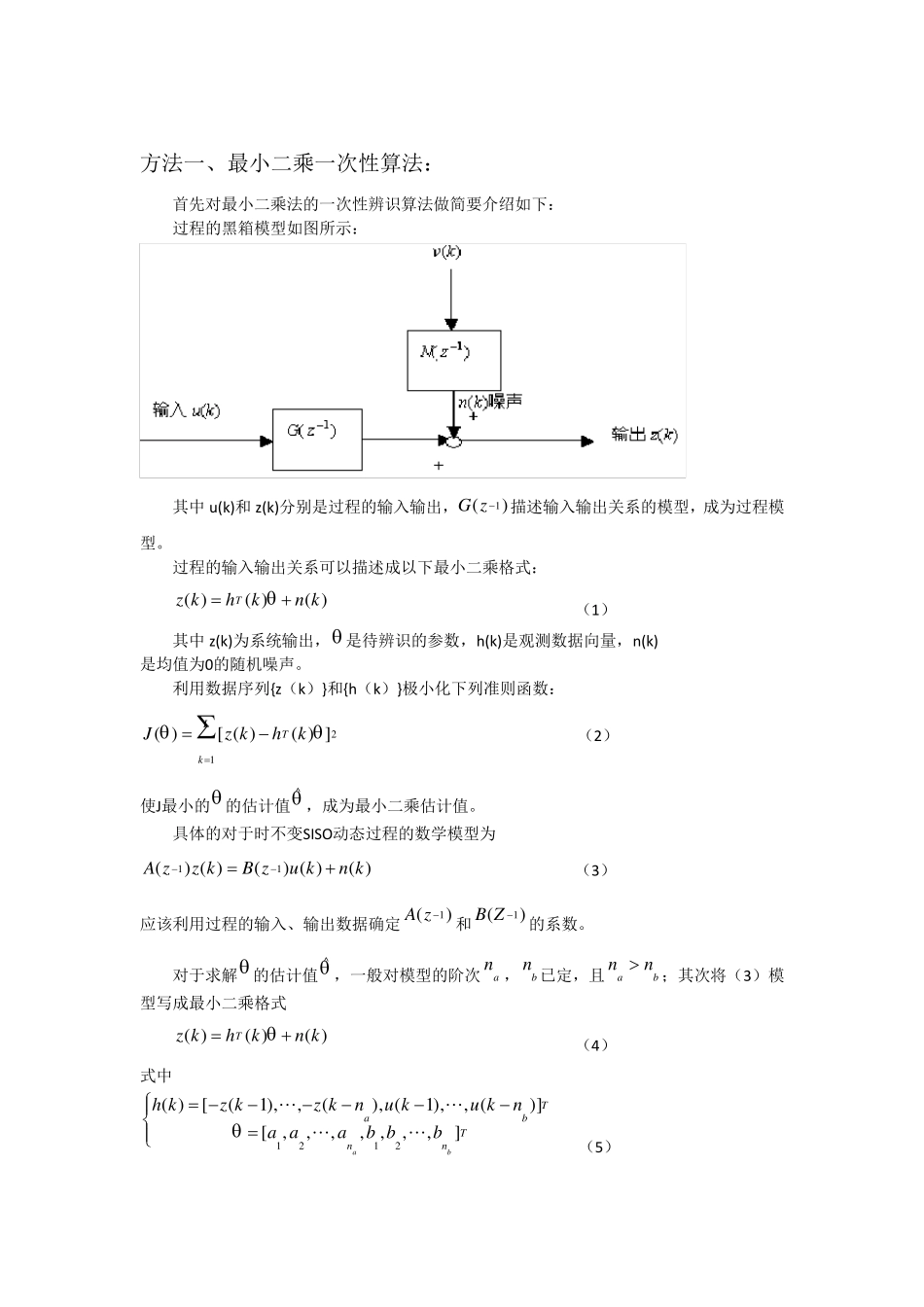
方法一、最小二乘一次性算法： 首先对最小二乘法的一次性辨识算法做简要介绍如下： 过程的黑箱模型如图所示： 其中 u(k)和 z(k)分别是过程的输入输出，)(1zG描述输入输出关系的模型，成为过程模型。 过程的输入输出关系可以描述成以下最小二乘格式： )()()(knkhkzT （1） 其中 z(k)为系统输出， 是待辨识的参数，h(k)是观测数据向量，n(k) 是均值为0的随机噪声。 利用数据序列{z（k）}和{h（k）}极小化下列准则函数： LkT khkzJ12])()([)( （2） 使J最小的 的估计值^ ，成为最小二乘估计值。 具体的对于时不变SISO动态过程的数学模型为 )()()()()(11knkuzBkzzA （3） 应该利用过程的输入、输出数据确定)(1zA和)(1ZB的系数。 对于求解 的估计值^ ，一般对模型的阶次an ，bn 已定，且bann ；其次将（3）模型写成最小二乘格式 )()()(knkhkzT （4） 式中 TnnTbababbbaaankukunkzkzkh],,,,,,,[)](,),1(),(,),1([)(2121 （5） Lk,,2,1 因此结合式（4）（5）可以得到一个线性方程组 LLLnHZ （6） 其中 TLTLLnnnnLzzzz)](),2(),1([)](),2(),1([ （7） 对此可以分析得出，LH 矩阵的行数为),max(ba nnL ，列数bann 。 在过程的输入为2n阶次，噪声为方差为1，均值为0的随机序列，数据长度)(bannL的情况下，取加权矩阵L为正定的单位矩阵I，可以得出： LTLLTLzHHH1^)( （8） 其次，利用在Matlab中编写M文件，实现上述算法。 此次算法的实现，采用6阶M序作为过程黑箱的输入；噪声采用方差为1，均值为0的随机数序列；黑箱模型假设为：y(k)-1.5y(k-1)+0.7y(k-2)=2u(k-1)+0.5u(k-2)，则系统输出为Z(k)-1.5Z(k-1)+0.7Z(k-2)=2U(k-1)+0.5U(k-2)+n（k）；模型的阶次2,2bann；数据长度取L=200。 程序清单如下见附录：最小二乘一次性算法Matlab程序 运行结果如下： 图1 最小二乘一次性算法参数真值与估计值 其中re为真值，ans为估计值^ 结果发现辨识出的参数与真值之间存在细微误差，这是由于系统噪声以及数据长度L的限制引起的，最小二乘辨识法是一种无偏估计方法。 方法二、最小二乘递推算法： 最小二乘一次性算法计算量大，并且浪费存储空间，不利于在线应用，由此引出最小二乘参数估计的递推算法，其基本思想是按观测次序一步一修正，即： ^^^'(1)( )[ ( )(...