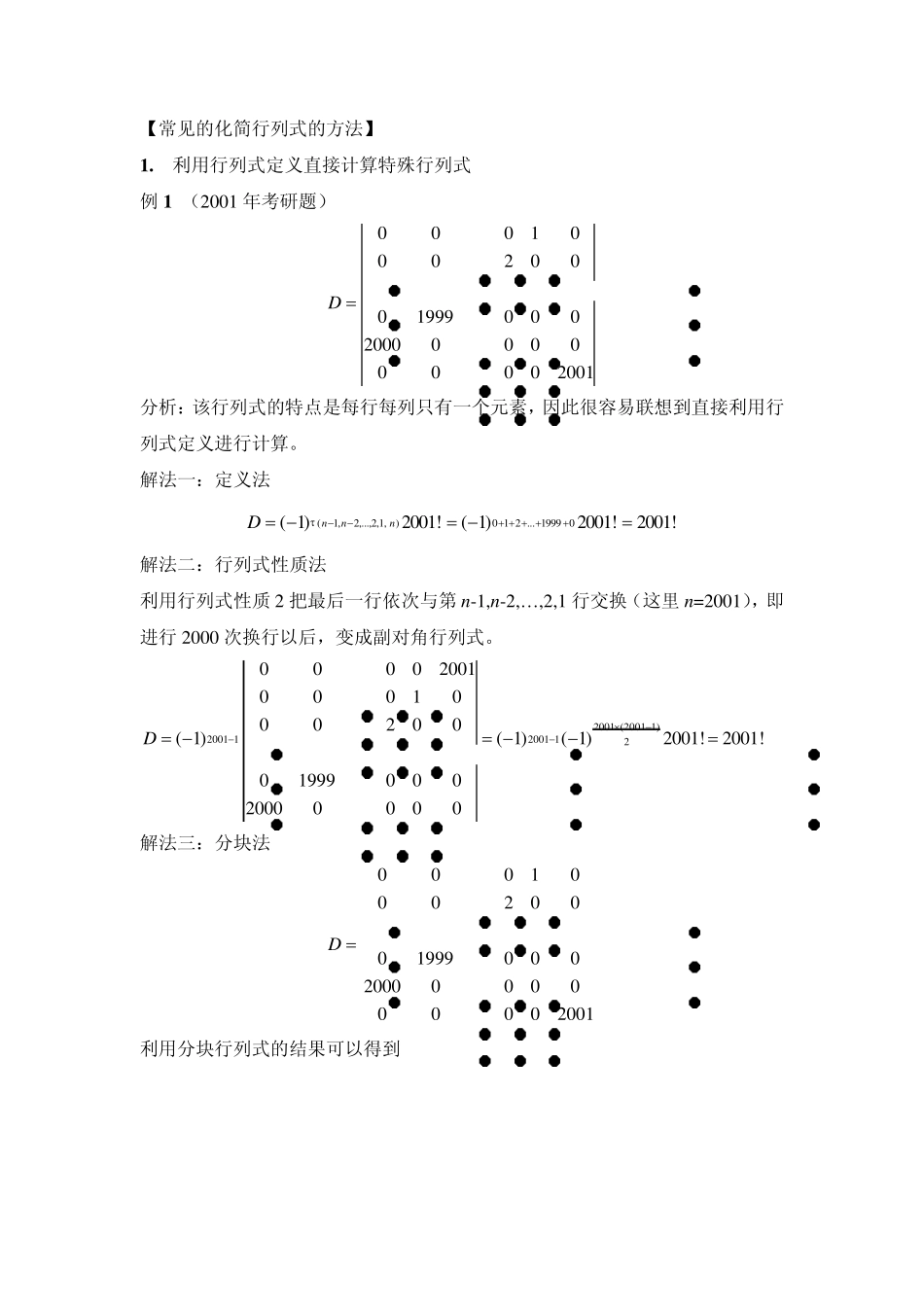
特殊行列式及行列式计算方法总结 一、 几类特殊行列式 1. 上(下)三角行列式、对角行列式(教材P7 例5、例6) 2. 以副对角线为标准的行列式 11112112,1221222,11,21,11,112,1(1)212,110000000000000000000( 1)nnnnnnnnnnnnnnnnnnnnn nnnnaaaaaaaaaaaaaaaaaaaa aa 3. 分块行列式(教材P14 例10) 一般化结果: 00nn mnn mnmm nmm nmACAABBCB 0( 1)0n mnn mnmnnmmm nmm nACAABBCB 4. 范德蒙行列式(教材P18 例12) 注:4 种特殊行列式的结果需牢记! 以下几种行列式的特殊解法必须熟练掌握!!! 二、 低阶行列式计算 二阶、三阶行列式——对角线法则 (教材P2、P3) 三、 高阶行列式的计算 【五种解题方法】 1) 利用行列式定义直接计算特殊行列式; 2) 利用行列式的性质将高阶行列式化成已知结果的特殊行列式; 3) 利用行列式的行(列)扩展定理以及行列式的性质,将行列式降阶进行计算——适用于行列式的某一行或某一列中有很多零元素,并且非零元素的代数余子式很容易计算; 4) 递推法或数学归纳法; 5) 升阶法(又称加边法) 【常见的化简行列式的方法】 1 . 利用行列式定义直接计算特殊行列式 例1 (2001 年考研题) 0001000200019990002000000000002001D 分析:该行列式的特点是每行每列只有一个元素,因此很容易联想到直接利用行列式定义进行计算。 解法一:定义法 (1,2,...,2,1,)0 1 2 ... 1999 0( 1)2001!( 1)2001!2001!nnnD 解法二:行列式性质法 利用行列式性质 2 把最后一行依次与第 n-1,n-2,…,2,1 行交换(这里 n=2001),即进行2000 次换行以后,变成副对角行列式。 2001 (2001 1)2001 12001 12000020010001000200( 1)( 1)( 1)2001!2001!0199900020000000D 解法三:分块法 0001000200019990002000000000002001D 利用分块行列式的结果可以得到 2000(2000-1)200010020=2001=2001 (-1)2000!=200101999002000000D! 解法四:降阶定理展开 按照每一行分别逐次展开,此处不再详细计算。 2 . 利用行列式的性质将高阶行列式化成已知结果的特殊行列式 例 2 1111111111111111aaDbb 分析:该行列式的特点是 1 很多,可以通过12rr和34rr来将行列式中的很多 1化成 0. 解: 214143...