线性代数考试题及答案3VIP免费

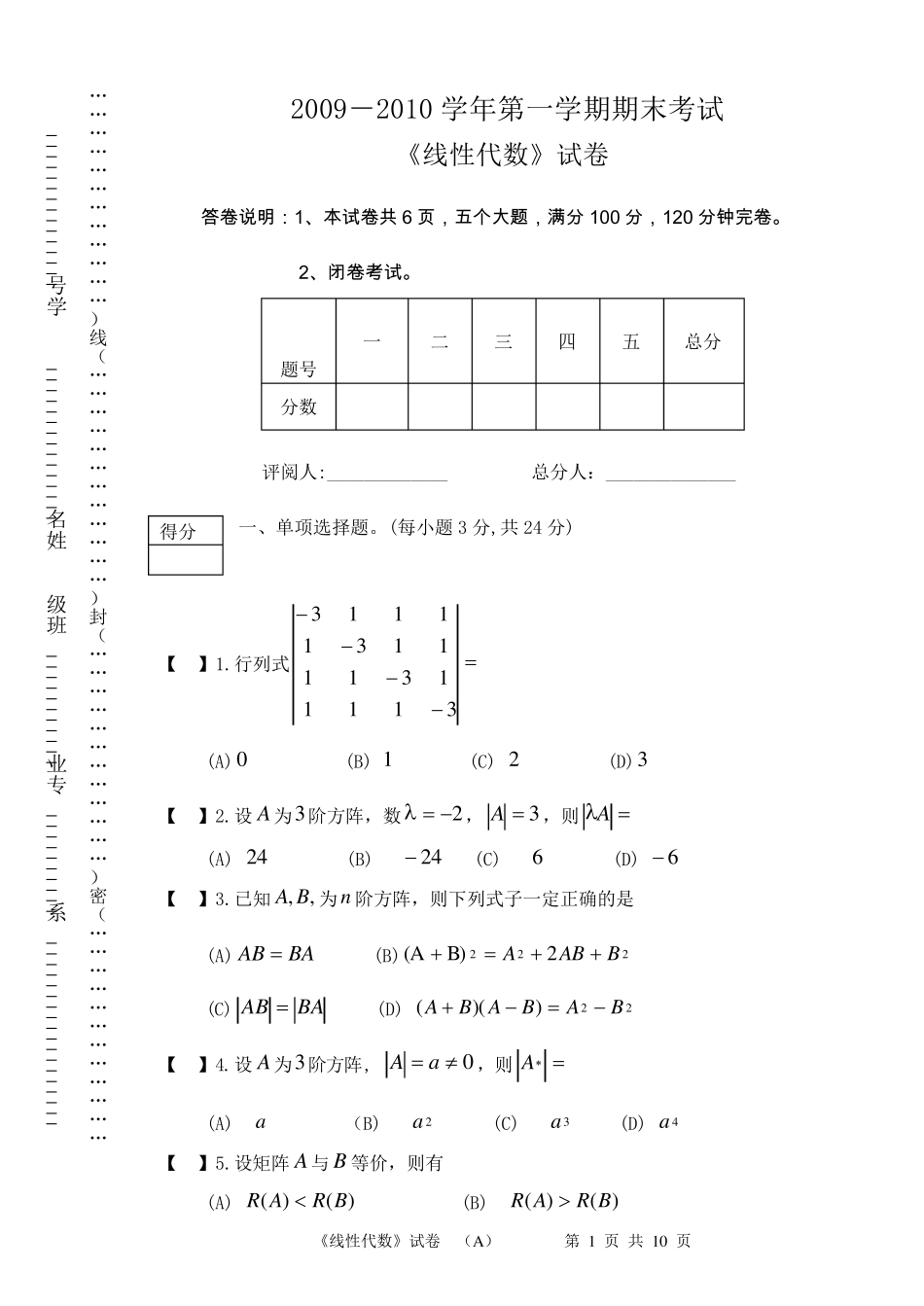
《线性代数》试卷 （A） 第 1 页 共 10 页 2009－2010 学年第一学期期末考试 《线性代数》试卷 答 卷 说 明 ： 1、本试卷 共 6 页，五个大题，满分 100 分，120 分钟完卷 。 2、闭卷 考试。 题号 一 二 三 四 五 总分 分数 评阅人:_____________ 总分人：______________ 一、单项选择题。(每小题3 分,共24 分) 【 】1.行列式3111131111311113 (A)0 (B) 1 (C) 2 (D)3 【 】2.设A 为3阶方阵，数2，3A，则A (A) 24 (B) 24 (C) 6 (D) 6 【 】3.已知,, BA为n阶方阵，则下列式子一定正确的是 (A)BAAB  (B)2222B)(ABABA (C)BAAB  (D) 22))((BABABA 【 】4.设A 为3阶方阵, 0 aA，则A (A) a （B) 2a (C) 3a (D) 4a 【 】5.设矩阵A 与B 等价，则有 (A) )()(BRAR (B) )()(BRAR 得分 __________________系__________专业___________班级 姓名_______________ 学号_______________ ………………………………（密）………………………………（封）………………………………（线）……………………………… 《线性代数》试卷 （A ） 第 2 页 共 10 页 (C) )()(BRAR (D) 不能确定)(AR和)(BR的大小 【 】6.设n 元齐次线性方程组0Ax的系数矩阵A 的秩为r ，则0Ax有非零解的充分必要条件是 (A) nr  (B) nr  (C) nr  (D) nr  【 】7. 向量组)2(,,,21maaam线性相关的充分必要条件是 (A) maaa,,,21中至少有一个零向量 (B) maaa,,,21中至少有两个向量成比例 (C) maaa,,,21中每个向量都能由其余1m个向量线性表示 (D) maaa,,,21中至少有一个向量可由其余1m个向量线性表示 【 】8. n 阶方阵A 与对角阵相似的充分必要条件是 (A)nAR)( (B) A 有n 个互不相同的特征值 (C) A 有n 个线性无关的特征向量 (D) A 一定是对称阵 二、填空题。(每小题 3 分,共15 分) 1.已知3 阶行列式 D 的第2 行元素分别为1,2,1 ，它们的余子式分别为2,1,1 ，则D 。 2.设矩阵方程12640110X，则X 。 3.设x是非齐次线性方程组bAx 的一个特解，21,为对应齐次线性方程组0Ax的基础解系，则非齐次线性方程组bAx 的通解为 . 4.设nm 矩阵A 的秩 rAR)(，则n 元...