结构力学第五章习题及答案VIP免费

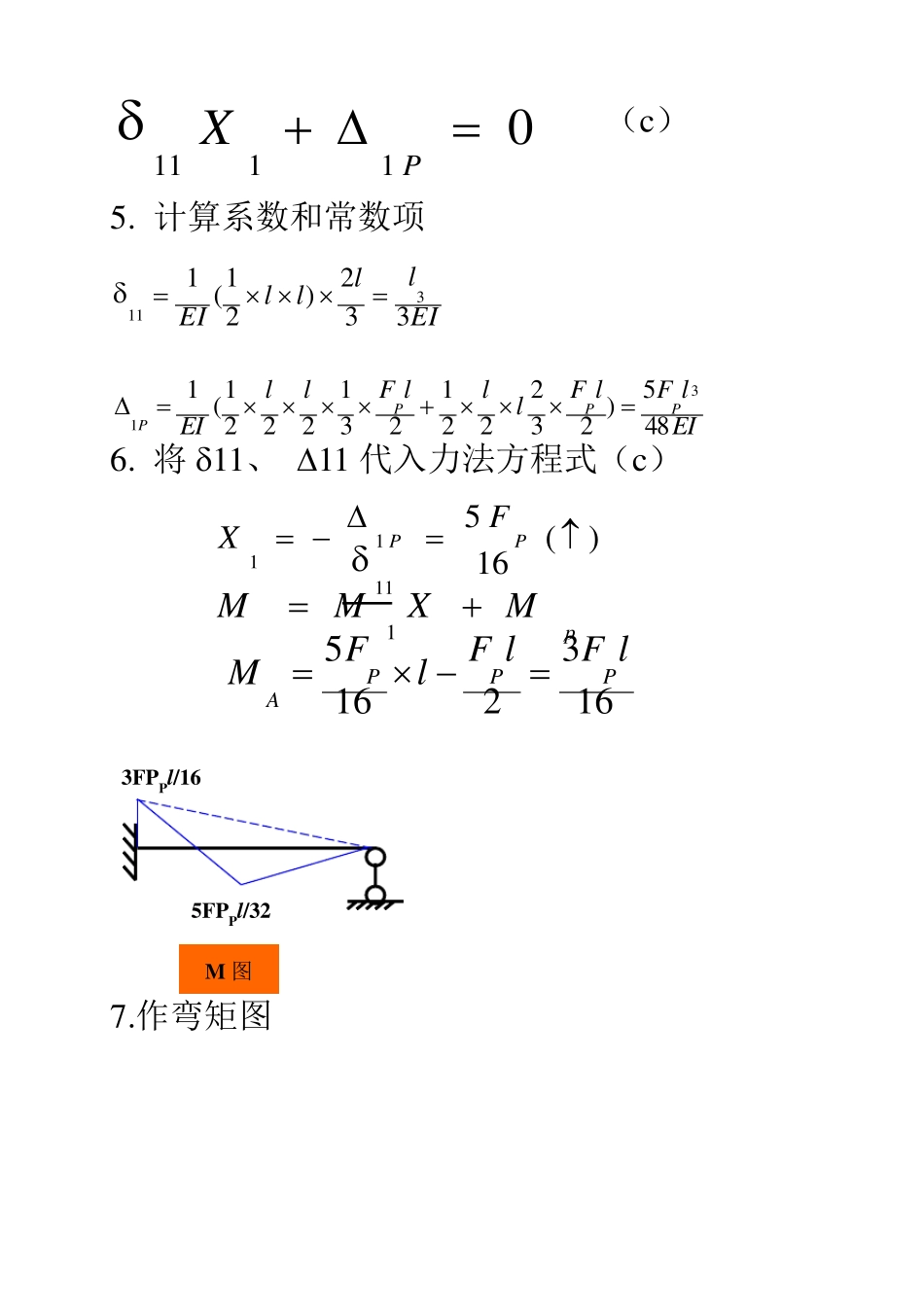
第五章 习题 5—2 试用力法计算下列结构，并会出弯矩图。 解：1.判断超静定次数：n=1 2. 确定(选择)基本结构。 3.写出变形(位移)条件： （a） 根据叠加原理，式（a）可写成 （b） 4 .建立力法基本方程 将∆11=11x1代入(b)得 FP A B C l/2l/2(a) FP X1 X1=1 M1 图 基本体系 MP 图 l FP FPl/2 EI 01 01111P（c） 5. 计算系数和常数项 EIllllEI332)21(1311 6. 将11、 ∆11 代入力法方程式（c） 7.作弯矩图 3FPPl/16 5FPPl/32 M 图 01111PXEIlFlFlllFllEIPPPP485)2322212312221(131)(1651111PPFXpMXMM11632165lFlFlFMPPPA 解：1.判断超静定次数：n=1 2. 确定(选择)基本结构。 3.写出变形(位移)条件： （a） 根据叠加原理，式（a）可写成 （b） 4 .建立力法基本方程 将∆11=11x1代入(b)得 （c） 5. 计算系数和常数项 EI2 EI1 FP A B X1 X1=1 FP C (b) M1 图 基本体系 MP 图 l FP(l-a） 01 01111P01111PX133)3221(1)]332()(21)332()(21[132331211EIaEIalaaaEIalaallaaalEI22216)2()(]3)(2)(213)()(21[1EIalalFalFaalalFaalEIPPPP 6. 将11、 ∆11 代入力法方程式（c） 31233231)1(322aIIlaallFXP 7.作弯矩图 （d）解： 超静定次数为2 选择基本结构如图（1）所示力法典型方程为： 11X1+12X2+△1P=0 21X1 + 22X2+△2P=0 计算系数和常数项，为此作作出 X1=1、X2=1 和荷载单独作用下的弯矩图如（2）（3）（4）所示计算结果如下 pMXMM11(a) EIlllllllEI34)3221(1311 EIllllEI2)2(1312 1212 EIllllEI3)3221(1322 EIq lllq llq llEIP85)243231(14221 EIq lllq lEIP4)22(1422 将以上各系数代入方程(a) 04320852344231342313EIq lXEIlXEIlEIq lXEIlXEIl 解联立方程得 X1=3q l/7 (↑) X2=3q l/28(←) 最后绘制弯矩图 M 如（5）所示。 q X 1 X 2 基本结构 （1） X 1=1 l l （2） X 2=1 l 图1M图2M（3） q l2/28 q l2/4 M图 （4） B A C EI q l l EI （d）原结构 q l2/2 q l2/2...